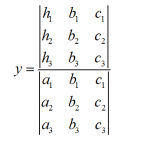Our site offers a wide variety of Math Help resources, including hundreds of Statistics, Calculus, Algebra, Decision Analysis and Finance calculators with steps. So please search around to find what you need. We are continuously adding new tutorials and lessons, solvers, online calculators and solved math problems.
The math help we provide is mostly suitable forcollege and high school students, even though we believe that there is a little bit for everyone. We can help you with the following subjects:




Search our Math and Stats Help tutorials, online solvers and calculators with the navigation menus on the top of the page, or you can search what you need in the search box below:
Our Mission
Mathcracker aims to help YOU LEARN math by giving you access to learning tools. Our belief is that Math is fundamental to understanding and functioning in the modern world, plus, math is also pretty neat. Our desire is to make math accessible to everyone in an open-access, democratic environment, by helping you to learn – and do – math using our tools, solvers, articles.
The Mathcracker project is situated within the Multiliteracies paradigm, which posits that changes in technology are changing how education, learning, and being work. The digital tools provided throughout Mathcracker can help your mathematical literacies take shape and help make you a better learner, thinker, and practitioner, in whatever your field may be. So, enjoy! Feedback helps us make your experience better, so please send us your thoughts and ideas at mathcracker0@gmail.com.
Latest Tutorials
 Welcome Mathcracker 2.0
Welcome Mathcracker 2.0February 3rd, 2021
Finally! We are very pleased to announce the new version of the site. We have added new exciting features such a crisp new graph designs, with a thorough review of the content and materials.
● And we have added a much anticipated feature: now you will be able to download the step-by-solutions our calculators provide in a Word (docx) file.
● We have also added a premium membership that allows you to get access to our content and solver/calculators, without any ads.
● Also, our members will have access to a 30,000+ collection of step-by-step sample solved Math and Stats problems.
● And many other features to be unveiled throughout the year, including artificial intelligence, automated worksheets, lessons and practice, along with automated detection and solution of problems.
Welcome 2020January 3rd, 2020
This year is the year where MathCracker will make a substantial leap in terms of the content offered in the site. So, keep tuned for more math solvers, calculators and lessons, and all the success in this new academic year.
Factoring ExpressionsAugust 1st, 2019
This in depth and meaty tutorial will help you understand how to factor algebraic expressions.
Learn How to Simplify RadicalsAugust 1st, 2019
Simplifying radicals gotta be THE most useful thing to know about in Basic Algebra. Learn about it in this tutorial.
Dealing with Negative ExponentsJuly 20th, 2019
Among all things related to the rules of exponents, students tend to get confused when dealing with negative exponents. This tutorial will clarify all your doubts.
Rules of ExponentsJuly 20th, 2019
One of the crucial skills required to deal with algebraic expression is the proper use of rules of exponents.
Cramer's RuleJuly 4th, 2019
All you need to know about Cramer's Rule and how to use it to solve systems of linear equations.
The Binomial TheoremJuly 4th, 2019
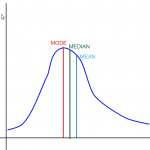
One of the most ubiquitous theorems in Math: The Binomial Theorem. Learn how to easily compute the binomial coefficients. The Mean, the Median and the Mode
July 4th, 2019
See this tutorial to learn how to and when to use the mean, median or mode as the measure of center, depending on the type of distribution.
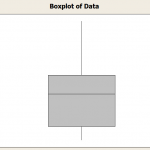
The Box-and Whisker PlotJune 5th, 2019
What is a Box and Whisker Plot? How do you define the box? The Whiskers? Find out in this tutorial.
The EllipseMay 28th, 2019
And to conclude the series on conic sections, it is now time for the ellipse.
The HyperbolaMay 28th, 2019
We continue our series of tutorial on conic sections. This time, it is the turn of the hyperbola.
The ParabolaMay 24th, 2019
Conic sections and the general equation of the parabola.
Partial Fractions DecompositionMay 23th, 2019
A very complete and in depth tutorial on partial fractions decompositions, with concrete steps to follow.
Logarithmic RulesMay 22th, 2019
A complete tutorial of how to apply log rules, with explanations and examples.
Order of OperationsMay 22th, 2019
Take a look at this tutorial about PEMDAS and the convention for the order of operations.
The Graph of a FunctionMay 21th, 2019
Learn more about all the concepts related with the graph of a function.
The Unit CircleMay 21th, 2019
One of the most versatile Math artifacts: See how the unit circle crosses Algebra, Geometry and Trigonometry.
Domain and RangeMay 20th, 2019
Crucial concepts when dealing with functions: Domain and Range.
Absolute ValueMay 19th, 2019
Another great, in-depth tutorial. All you need to know about the Absolute Value of a number.
Commutative PropertyMay 18th, 2019
Here is another crucial property in Algebra: the Commutative Property.
Associative PropertyMay 18th, 2019
The associative property is one of those properties that is used all the time, but we do not really know.
Horizontal AsymptotesMay 17th, 2019
All there is to know about horizontal asymptotes.
Equation of the CircleMay 5th, 2019
Learn all that there is to the circle: The Equation of a Circle.
Finance SolversOctober 11th, 2018
We have started a new section for Finance solvers. Check them out: Future Value Calculator, Present Value Calculator, Present Value of an Annuity, among many other Finance Calculators.
Semester will Start SoonAugust 11th, 2018
One of the best advice right before starting a new semester: Don't panic.
Easy Stats, Hard Stats?August 3rd, 2018
Excellent article about why it is usually the easy Stats classes those where students need the most help with. Check it out!.
Busy preparing the MathCracker 2.0 launchJune 1st, 2018
Going for a large overhaul in the site, which much more powerful tools. In the meantime, here I leave you a new article Tricks of the Trade: Finding Stats Homework Help. Another interesting post about why more and more students end up learning their Stats using private tutors. Check it here. Also all, you need to know about the process finding help with your finance assignment.
Descriptive Statistics CalculatorsFebruary 28th, 2018
Although we already had a complete descriptive statistics calculator, I have requests to make some specific calculators, to compute one measure at a time, so here I have it: I added a mean calculator, standard deviation calculator and median calculator.
New Section of Education ArticlesFebruary 20th, 2018
I have added a page that puts together all the articles we have available about education topics. Also, I found this interesting article about the advantages of staring with Algebra early in life.
SPSS TutorialSeptember 20th, 2017
Check our revised SPSS tutorial.
Statistics CalculatorsAugust 17th, 2017
I have added a couple of algebraic solvers for arithmetic sequences and geometric sequences.
Statistics CalculatorsAugust 15th, 2017
Z-scores are the way we compute normal probabilities, as any general normal distribution can always be reduced to a standard normal distribution. Check out this Z-Scores Calculator.
Statistics TutorialsAugust 2nd, 2017
I have found two excellent tutorials one about hypothesis testing, and the other one about statistics and parameters. Both are great reads.
Several Effect Size CalculatorsJuly 31st, 2017
I have added several effect size calculators, including a Gamma Calculator and a Phi Coefficient Calculator.
Cramer's V CalculatorDecember 25th, 2016
The idea of "effect size" is very relevant in statistics. If often happens that a test statistics is significant, but the association has no practical meaning. This is because a extremely large sample size alone can find significant n extremely small effect. Cramer's V is a statistic that assess the effect size or practical significance of the association between nominal variables. Check it out: Cramer's V Calculator.
Calculator of the Area and Volume of a PyramidDecember 5th, 2016
More solvers for our series of elementary geometry solvers, and we now add a calculator of the area and volume of a square pyramid that will show you all the steps and formulas used to calculate the surface area and volume of a square pyramid of side \(l\) and height \(h\).
Calculator of the Area and Volume of a CubeDecember 4th, 2016
We continue our series of elementary geometry solvers, and we now add a calculator of the area and volume of a cube that will show you all the steps and formulas used to calculate the area and volume of a cube of side \(l\).
Calculator of the Area and Volume of a Cone
November 30th, 2016
Keeping the momentum up, here you have a calculator of the area and volume of a conethat will show you all the steps and formulas used to calculate the area and volume of a right circle cone radius \(r\) and height \(h\).
Calculator of the Area and Volume of a SphereNovember 30th, 2016
Another solver for our Geometry series, a calculator of the area and volume of a sphere that will show you all the steps and formulas used to calculate the area and volume of a sphere of radius \(r\).
Critical Correlation CalculatorNovember 29th, 2016
Typically found in special tables, here you have a critical correlation calculator. The advantage of this calculator is that it will compute the critical correlation for any value of \(n\), which is not always possible when you use critical correlation tables, which only have a few values of \(n\).
Geometry SolversNovember 28th, 2016
Lots of people were asking for geometry solvers and here they are. I have started a new section for Geometry and I'll be adding more solver on a continuous basis. For now, here I leave for you a area and perimeter of a circle calculator, and an area and volume calculator for cylinders
Polynomial Operations CalculatorNovember 25th, 2016
This one is a solver that user were clamoring for: Let me introduce our Polynomial Operations Calculator, with which you can add, subtract and multiply polynomials, with the solution shown step-by-step. Also, we have started with MathQuill, and excellent option for enhancing the input of math.
Absolute Value CalculatorNovember 23th, 2016
We expand even more our Algebra series with some more basic solvers, in this case, a absolute value calculator.
Algebraic Expression CalculatorNovember 19th, 2016
New solver in our Algebra series, now I have added a solver that evaluates all sort of algebraic expressions that can include any kind of operation (sum, subtraction, multiplication, division), numbers, fractions, trigonometric functions, exponential functions, powers, roots, etc. Check our Algebraic Expression Calculator.
Fraction Operations CalculatorNovember 19th, 2016
Continuing the series of Algebra solvers, I have added a solver that calculates operations between fractions and shows all the steps. Depending of the operation required it conducts the appropriate steps to reach the final fraction result, in reduced form. Check out our fraction operation solver.
Function GrapherNovember 17th, 2016
I have made a new function grapher to replace the old flash grapher we had. This time, I used the Google Chart format, that looks more modern and goes along the trend of JS charts.
Fraction ReductionNovember 13th, 2016
I get a lots of requests for this one, so here it goes. This is a fraction reduction tool fraction-reduction-lowest-terms.php, that takes a fraction into its lowest terms.
Next Algebra Solver in our seriesNovember 12th, 2016
This time, I added a greatest common divisor, or as it usually known as greatest common factor calculator . I took care to provide as much detail as possible in the calculations shown by the solver.
New Algebra SolverNovember 11th, 2016
Today I start with a new series of Algebra solvers. I have added a prime decomposition calculator, you type in a positive integer number and the solver tell you in a detailed way what is its prime decomposition.
New Site DesignSeptember 8th, 2016
I am very pleased to announce that we have rolled a new site design, with a much improved mobile functionality.
More Math CracksJanuary 31th, 2016
This time I decided to write on functions and how to deal with them.
Another Math ArticleJanuary 20th, 2016
Another article. This time dealing with the possibility of having a software that can solve Math and Stats problems FULLY automatically Check Here.
Another Math CrackJanuary 5th, 2016
I loved the feedback I got from the first Math Crack, so I decided to pump up the series. I'll be uploading them periodically. This next first Math Crack is about an easy explanation of derivatives.
Math CracksJanuary 5th, 2016
I finally started a project that I have been wanting to undertake for a while. It is the Math Cracks, which is the way I call to this short tutorials that attempt to explain hard math concepts in simple terms, step-by-step. The first Math Crack of the series is Integration by Parts.
Site upgradeApril 21th, 2015
A site update is coming soon. I will be changing the layout a bit so that to keep the solvers in a more organized way and the articles will be organized rather in blog format. I will be adding a complete set of Algebra solvers, so stay tuned.
More solversFebruary 4th, 2015
A couple of tutorials and solvers were added: Quadratic Formula: The meaning of the term -b/2a, an article about Algebra 2 and a Line Plot Maker
More ArticlesJanuary 28th, 2015
I have added a couple of new articles for your reading enjoyment: Math Articles
Minimum Sample SizeDecember 7th, 2014
I have added a minimum sample size calculator for mean and proportion
Many stats calculatorsDecember 5th, 2014
After long working hours, I've finished all the solvers required to cover all basic statistics topics. The new solvers are: Z-test for two means, Z-test for two proportions, T-test for two means, T-test for paired samples, Chi-Square Goodness of fit, and Chi-Square test of Independence. I also added the most important non-parametric tests, which are the Sign Test, also Wilcoxon Signed Ranks Test, as well as the Wilcoxon Rank-Sum Test and Kruskal-Wallis
Online Accounting CoursesNovember 12th, 2014
I get asked to review different online curricula. Thanks to a guest writer, I just added a great article about online accounting curricula. You can check it here.
Accounting HelpNovember 11th, 2014
Found a very informational article about the do's and dont's of Accounting Homework Help. You can check it here.
NewsNovember 11th, 2014
Great changes to improve user experience are coming very soon. I have written recently many math and stats solvers that I'll be adding to the site. I've been polishing the scripts we already have and this is almost turning into a full time job. As many users are aware, we have had ads for the last few months, and even though I don't like ads, it is the only way to support the site, which is turning into a full time job by now. I'm looking for a more efficient way of using ads so that the site can be ad-supported and it continue being free that way.
Various Statistical TestsNovember 2nd, 2014
More Stats tests done. I have finished a t-test for one population mean with unknown population standard deviation and a Chi-Square test for one population variance. Pretty much as the other solvers I have added, they are simple to use: define hypotheses, and parameters of the test, and a detailed step-by-step calculation is performed.
Z-testsOctober 31st, 2014
I've been working on these for a while and I finally finished them. I added a z-test for one population mean and a z-test for one population proportion. Very user friendly, define hypotheses, and parameters of the test, and a detailed step-by-step calculation is performed. Recommended.
Histogram MakerOctober 20th, 2014
I just added a working histogram maker. You enter the dataset and the number of bins and a properly scaled histogram is rendered by the script.
Bar Graph MakerOctober 9th, 2014
I have added a very cool bar graph maker. You enter the categories, the values associated with each of the categories, and a bar chart rendered by the script.
Mortgage CalculatorOctober 8th, 2014
Not exactly the typical calculator we do, but I have had some requests for it, so I added a simple mortgage calculator tool to compute the monthly payment for a mortgage, under basic assumptions (without considering PMI and insurance).
New math solverOctober 4th, 2014
I have uploaded a 2x2 system of linear equations solver.
UpdateOctober 4th, 2014
I have updated the pie chart maker script.
Confidence Interval CalculatorsOctober 2st, 2014
I have added two confidence interval calculators. They are confidence intervals for the population mean μ when the population standard deviation σ is known and for when the and a population standard deviation is not known.
Two more more probability calculatorsOctober 1st, 2014
We have two more probability calculators. They are a binomial distribution calculator and a Poisson distribution calculator.
Added two more probability calculatorsSeptember 30th, 2014
I have added two new probability calculators, based on a couple of requests I had. They are a exponential distribution calculator and a uniform distribution calculator.
Tips for finding math helpSeptember 9th, 2014
I have added a new article. Check it out here.
Grade Calculator OnlineJune 9th, 2014
I have added a correlation coefficient calculator. This time, the script is more user friendly, and checks for errors in the data before processing them.
Grade Calculator OnlineJune 4th, 2014
I received a whole lot of e-mails asking for a tool to calculate grades. Well, I just did it. With this online grade calculator you are able to input your assignment/test scores and the calculator will tell your final score and final letter grade. And if you don't have all the grades, the calculator will tell you what score you need to get in your final assignment/test in order to get an A.
More materialJune 4th, 2014
After some time of silence, I'm back. As many of you know, I run this site on my spare time trying to keep it as updated as possible. I'm very pleased to see the positive effect the math tools we offer in our site are having in the community. Countless e-mails thanking me for the work I put in the site make me want to keep working even harder. The free online math calculator we provide in the site have even been used as references in scientific papers. That is very cool indeed! I have great plans for the site. Keep visiting.
Discount for math helpSept 25rd, 2013
Our good friends at MGT are giving specially for us this 15% discount code for their online math homework help services: mthcrk1501 . From references given by users of our community, they are very reliable.
Summer is overSept 24rd, 2013
Summer is over, and time is back for some math. We have great plans for this year. Our aim is to offer the best quality free math help, for which reason we will continue adding more and more useful content. We also expect to materialize some very interesting partnerships. Stay tuned!
More Online Stats calculatorsMay 24rd, 2013
As promised, a couple of critical values calculators have been added: z-distribution critical values and t-distribution critical values
New Online Stats calculatorMay 23rd, 2013
A t-distribution probability calculator was added. This is the first delivery of a series of scripts that will be added. Coming soon a couple of online calculators for critical values for the z-distribution and the t-distribution.
New ArticleMarch 8th, 2013
I just added an article about math problem solving techniques. See article
List of Calculus ProblemsMarch 8th, 2013
I found a new site offering sample solved calculus problems: Calculus Problems
Scripts Fixed
January 30th, 2013
We have added more than 300 solved statistics problems
Scripts FixedJanuary 21th, 2013
Due to a problem with a configuration file the scripts in the site were not working for a while, now they are working fine. Sorry for the inconvenience.
New TutorialDecember 18th, 2012
A good tutorial about the normal distribution was added. The normal distribution and the standard normal distribution
More Solved Statistics ProblemsDecember 7thd, 2012
I added a good list of solved statistics problems.
Fixed scatterplot tool and added regression line toolNovember 3rd, 2012
I made a few adjustments to the scatterplot module, and added a new regression line tool, to complement the existing tool. Linear Regression Calculator
Free Statistics Help ResourceSeptember 29th, 2012
This new resource seems to be very useful, you may find it interesting to take a look Free Statistics Help
Site back upApril 27th, 2010
The site is back up online. For problems out of my control the site was down for a couple of weeks. We'll be back with new material. Thanks to everyone.
New section addedMay 17th, 2008
I have found a good collection of free solved math problems and math answers.
In case you have any suggestion, please do not hesitate to contact us.
Interesting Math Help Links
- » Interesting Math problems
- » S.O.S. Math
- » Math Portal
- » Fact Monster
- » Math Homework Help
- » Statistics Homework Help
- » Calculus Help
- » Math Problems
- » Free Statistics Help
- » Economics Help
- » Social Sciences Help
- » Geometry Help
If you think that our site could be of use to your website's visitors you can link to our free math help site: Link to us
Other interesting links
• Get a dissertation statistics writing service online at an affordable price.• Need dissertation statistics help from a professional.
• Keep abreast of the latest academic news and stay effective in your remote studies with high-quality math homework help online.
• If you're struggling with complex math concepts and elaborated formulas, professional experts may come in handy - simply drop them a message "do my math homework" and forget your worries!
• Rent a Windows VPS from VPSServer.com for your complex math calculations. Benefit from their high-performance infrastructure to optimize computational tasks efficiently.
• Get the help of expert statistics consultants for any kind of statistics project (SPSS, Stata, SAS, R, Excel, Minitab, Eviews).
• Stressed about deadlines? Simply say 'write my essay' and watch our professionals craft your perfect paper!.
• When only the best will do, count on our top essay writing team to elevate your papers!.
• Get quality help with math assignment today
In case you have any suggestion, or if you would like to report a broken solver/calculator, please do not hesitate to contact us.