Quadratic Equation Solver

This calculator will allow you calculate a quadratic equation that you provide, showing all the steps. All you need to do is to provide a valid quadratic equation.

It could be something that is already simplified and ready to solve like x^2 + 3x + 5 = 0, you can provide something is not readily simplified like 3x^2 - 4x + 5/3 = x^2 +1/3x -1, for example .

Once you provide a valid quadratic equation, all you need to do is to click on "Calculate", and you will be provided with all the steps of the process to calculate the roots of the quadratic equation that is provided.

Usually, you will use the quadratic formula to calculate quadratic equations, but that is not the only way, as we will see in the following sections.

How to calculate a quadratic equation?

There are several strategies to solve quadratic equations. The most commonly used one is the use of the quadratic formula. Also, you can solve by completing squares, or you can solve by quadratic factoring.

What are the steps for calculating quadratic equations using the quadratic formula?

• Step 1: Identify the quadratic equation that you want to calculate
• Step 2: Make sure that the equation is fully simplified, otherwise proceed with the simplification, until you have an equation of the form ax² + bx + c = 0
• Step 3: After the equation is reduced to its simplified form, you can use the quadratic formula: \(x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

Possibly, using the quadratic equation formula is the most practical way of finding the roots of a quadratic equation, but there are other reasons why you would you other methods.

How to solve a quadratic equation by completing squares?

The second most common way of solving a quadratic equation is by using the technique of completing squares. There is not really a formula for completing squares (although technically there is one, based on the solutions of the quadratic equation), and it rather a process.

What are the steps for completing squares

• Step 1: Identify the quadratic equation that you want to solve
• Step 2: You need to make sure that the equation is fully simplified, and that you have an equation of the form ax² + bx + c = 0
• Step 3: Add and subtract a suitable term (in this case, (b/(2a))² to force the terms of the square of a binomial

The idea of the to force the appearance of a term of the form (x + "something)², which is the ultimate goal of completing squares.

Why would you use quadratic equations?

Quadratic equations appear constantly in the algebra applications are word problems. Solving quadratic equations is one basic core skill you need to acquire.

Then, in fields like Calculus, when computing maximization and minimization problems, you will need to have good familiarity with all types of quadratic equations.

Example: Solving a quadratic equation

Solve the following quadratic equation using the formula \(4x^2 + \frac{4}{3}x + 2 = 0\)

Solution: We need to solve the following given quadratic equation \(\displaystyle 4x^2+\frac{4}{3}x+2=0\).

For a quadratic equation of the form \(a x^2 + bx + c = 0\), the roots are computed using the following formula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In this case, we have that the equation we need to solve is \(\displaystyle 4x^2+\frac{4}{3}x+2 = 0\), which implies that corresponding coefficients are:

\[a = 4\] \[b = \frac{4}{3}\] \[c = 2\]

First, we will compute the discriminant to assess the nature of the roots. The discriminating is computed as:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{4}{3}\right)^2 - 4 \cdot \left(4\right)\cdot \left(2\right) = -\frac{272}{9}\]

Since in this case we get the discriminant is \(\Delta = \displaystyle -\frac{272}{9} < 0\), which is negative, we know that the given equation has two different conjugate complex roots.

Now, plugging these values into the formula for the roots we get:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{\left(\frac{4}{3}\right)^2-4\left(4\right)\left(2\right)}}{2\cdot 4} = \displaystyle \frac{-\frac{4}{3} \pm \sqrt{-\frac{272}{9}}}{8}\]

so then, we find that:

\[\displaystyle x_1 = \frac{-\frac{4}{3} - i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\] \[\displaystyle x_2 = \frac{-\frac{4}{3} + i \sqrt{\frac{272}{9}}}{8} = -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\]

Therefore, the given equation \(\displaystyle 4x^2+\frac{4}{3}x+2=0\) has two different conjugate complex roots, which are \(x_1 = \displaystyle -\frac{1}{6} - \frac{1}{6}\sqrt{17} i\) and \(x_2 = \displaystyle -\frac{1}{6} + \frac{1}{6}\sqrt{17} i\).

Graphically:

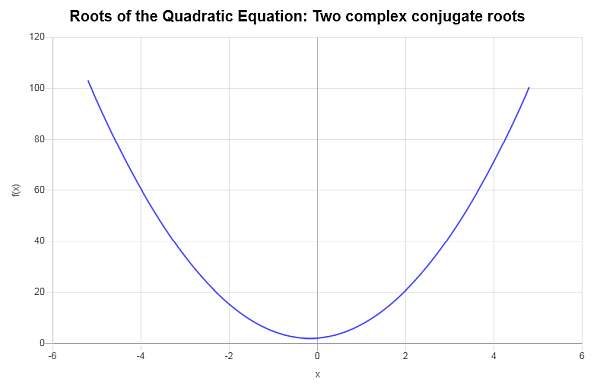
Example: Root of a quadratic equation

Find the roots of the following quadratic equation by completing squares \(2x^2 + \frac{1}{3}x + \frac{1}{72} = 0\)

Solution: In this case, we have that the equation we need to solve is \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72} = 0\), which implies that corresponding coefficients are:

\[a = 2\] \[b = \frac{1}{3}\] \[c = \frac{1}{72}\]

The discriminating is computed as:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{1}{3}\right)^2 - 4 \cdot \left(2\right)\cdot \left(\frac{1}{72}\right) = 0\]

Since in this case we get the discriminant is \(\Delta = \displaystyle 0 = 0\), which is zero, we know that the equation has only one real root.

Now, plugging these values into the formula for the roots we get:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{\left(\frac{1}{3}\right)^2-4\left(2\right)\left(\frac{1}{72}\right)}}{2\cdot 2} = \displaystyle \frac{-\frac{1}{3} \pm \sqrt{0}}{4}\]

so then, we find that:

\[x = \displaystyle \frac{-\frac{1}{3}}{4} = \displaystyle -\frac{1}{12}\]

Therefore, the given equation \(\displaystyle 2x^2+\frac{1}{3}x+\frac{1}{72}=0\) has only one real root, which is \(x = \displaystyle -\frac{1}{12}\).

Graphically:

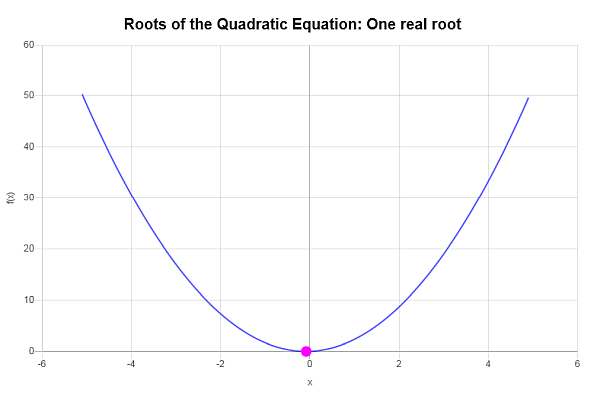
Example: Roots of equation calculation

Solve the following: \(3x^2 + \frac{2}{3}x - \frac{4}{3} = 0\)

Solution: For this example the equation we need to solve is \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3} = 0\), so then the corresponding coefficients are:

\[a = 3\] \[b = \frac{2}{3}\] \[c = -\frac{4}{3}\]

In this case, the discriminating is computed as:

\[\Delta = b^2 - 4ac = \displaystyle \left( \frac{2}{3}\right)^2 - 4 \cdot \left(3\right)\cdot \left(-\frac{4}{3}\right) = \frac{148}{9}\]

Since the discriminant is \(\Delta = \displaystyle \frac{148}{9} > 0\), which is positive, we know that the equation will have two different real roots.

Now, plugging these values into the formula for the roots we get:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\left(\frac{2}{3}\right)^2-4\left(3\right)\left(-\frac{4}{3}\right)}}{2\cdot 3} = \displaystyle \frac{-\frac{2}{3} \pm \sqrt{\frac{148}{9}}}{6}\]

so then, we find that:

\[ x_1 = -\frac{\frac{2}{3}}{6}-\frac{1}{6}\sqrt{\frac{148}{9}}=-\frac{1}{9}\sqrt{37}-\frac{1}{9} \] \[x_2 = -\frac{\frac{2}{3}}{6}+\frac{1}{6}\sqrt{\frac{148}{9}}=\frac{1}{9}\sqrt{37}-\frac{1}{9}\]

Therefore, the given equation \(\displaystyle 3x^2+\frac{2}{3}x-\frac{4}{3}=0\) has two different real roots, which are \(x_1 = \displaystyle -\frac{1}{9}\sqrt{37}-\frac{1}{9}\) and \(x_2 = \displaystyle \frac{1}{9}\sqrt{37}-\frac{1}{9}\).

Graphically:

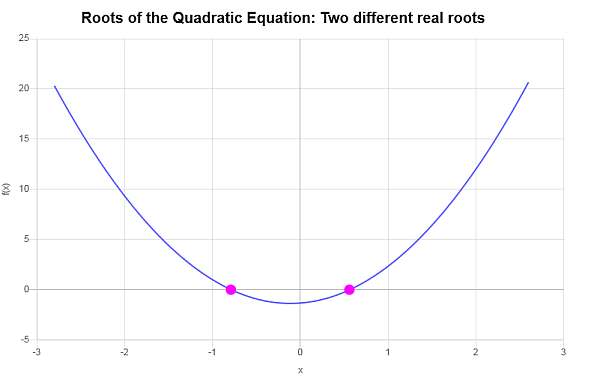
Other useful quadratic calculators

As we have seen in this tutorial, completing squares plays a fundamental role in calculating quadratic equations. Also, you can use this discriminant calculator to assess the nature of the roots (two real roots, one real root, or two complex roots) without solving the equation.

You can also use this vertex calculator to find the coordinates of the vertex of a quadratic equation, and find the axis of symmetry of a parabola. Also you can explore this quadratic factoring tool to explore yet another way of calculating quadratic equations.