Sum of Squares Calculator
Instructions: This Sum of Squares Calculator will help you compute the sum of squares associated to a set of sample data. Please provide the information required below:
What is the Sum of Squares?
The concept of sum of squares is a very useful one, which appears almost everywhere in Statistics, but people do not often take the time to explain what it is. So, starting from the beginning, the sum of squares usually refers to the sum of squared deviations with respect to the mean, for a sample of data.
How do you calculate the sum of squares?
Simple! Just take the square values of a list of given number, and add that up. Mathematically, the formula to define the sum of squares associated to the sample \(\{X_1, X_2, ..., X_n \}\) is:
\[ SS = \displaystyle \sum_{i=1}^n (X_i - \bar X)^2 \]Relationship Between Sum of Squares and Sample Variance
Why the idea of the sum of squares \((SS)\) is so useful in Statistics? Well, mostly for one reason: The sum of squares is a strong indication of the level of variability of a sample. And it is strongly related to the concept of sample variance. Indeed, the sample variance \(s^2\) is computed as:
\[s^2 = \displaystyle \frac{SS}{n-1}\]So, you take the sum of squares \(SS\), you divide by the sample size minus 1 (\(n-1\)) and you have the sample variance. That is neato.
The idea of sum of squares also extends to linear regression, where the regression sum of squares and the residual sum of squares determines the percentage of variation that is explained by the model. Similar situation applies to ANOVA.
Using Excel to Compute the Sum of Squares
How to calculate sum of squares in Excel? You probably should put your data in a column and label that column as "X", then compute the average for the sample, and create of column labeled "X - Xbar" which computes the value of a corresponding cell minus the average.
Then, use another column (next to the previous one) that labeled "(X - Xbar)^2", where you square the cells from the column to the left. Finally, the sum of squares is computed by adding up the values in the column. "(X - Xbar)^2".
Is this a Sum of squares calculator with steps
Yes, it is. All you need to do is to provide your sample data, in the form shown above. Then you just click the button and the calculator will show you all the tables, steps and conclusions relevant to the calculation.
Other statistics calculators
The concept of sum of squares has applications for the t-test for one sample , for the t-test for two samples and for regression , among many others.
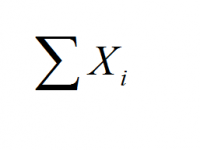
Sum of squares (SS) formula example
Question: Assume you have collected a random sample of size n = 16, and you have the following data: 4, 5, 3, 5, 2, 5, 3, 4, 5, 6, 12, 3, 2, 4, 5, 10. Compute the sum of squares (SS) for these data.
Solution:
These are the sample data that have been provided:
| \(X\) |
| 4 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 4 |
| 5 |
| 6 |
| 12 |
| 3 |
| 2 |
| 4 |
| 5 |
| 10 |
Based on the data above, the sample mean is computed as follows:
\[ \begin{array}{ccl} \bar{X} & = & \displaystyle \frac{1}{n} \sum_{i=1}^n X_i \\\\ \\\\ & = & \displaystyle \frac{1}{16} (4+5+3+5+2+5+3+4+5+6+12+3+2+4+5+10) \\\\ \\\\ & = & 4.875 \end{array}\]Now that we have the sample mean, we need to compute the square of the difference between each sample value \(X_i\) and the sample mean:
| \(X\) | \((X_i - \bar X)^2\) |
| 4 | \((4.875 - 4)^2 = 0.7656\) |
| 5 | \((4.875 - 5)^2 = 0.0156\) |
| 3 | \((4.875 - 3)^2 = 3.5156\) |
| 5 | \((4.875 - 5)^2 = 0.0156\) |
| 2 | \((4.875 - 2)^2 = 8.2656\) |
| 5 | \((4.875 - 5)^2 = 0.0156\) |
| 3 | \((4.875 - 3)^2 = 3.5156\) |
| 4 | \((4.875 - 4)^2 = 0.7656\) |
| 5 | \((4.875 - 5)^2 = 0.0156\) |
| 6 | \((4.875 - 6)^2 = 1.2656\) |
| 12 | \((4.875 - 12)^2 = 50.7656\) |
| 3 | \((4.875 - 3)^2 = 3.5156\) |
| 2 | \((4.875 - 2)^2 = 8.2656\) |
| 4 | \((4.875 - 4)^2 = 0.7656\) |
| 5 | \((4.875 - 5)^2 = 0.0156\) |
| 10 | \((4.875 - 10)^2 = 26.2656\) |
Based on the data above, the sum of squares \(SS\) is computed as follows:
\[ \begin{array}{ccl} SS & = & \displaystyle \sum_{i=1}^n {( X_i - \bar X - X_i )^2} \\\\ \\\\ & = & \displaystyle (4.875 - 4)^2 + (4.875 - 5)^2 + (4.875 - 3)^2 + (4.875 - 5)^2 + (4.875 - 2)^2 \\\\ \\\\ & & + (4.875 - 5)^2 + (4.875 - 3)^2 +(4.875 - 4)^2 + (4.875 - 5)^2 \\\\ \\\ & & + (4.875 - 6)^2 + (4.875 - 12)^2 + (4.875 - 3)^2 + (4.875 - 2)^2 + (4.875 - 4)^2 \\\\ \\\\ & & + (4.875 - 5)^2 + (4.875 - 10)^2 \\\\ \\\\ & = & 107.75 \end{array}\]Therefore, based on the data provided, the sum of squares is \(SS = 107.75 \).