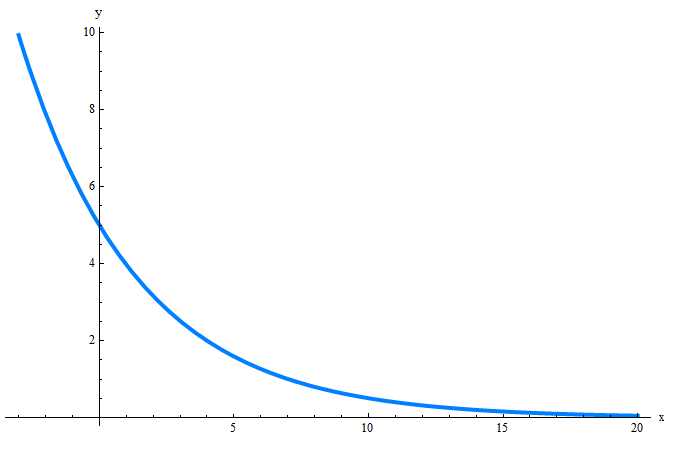
Exponential Function Calculator from Two Points

The idea of this calculator is to estimate the parameters $A_0$ and $k$ for the function $f(t)$ defined as:

$$f(t) = A_0 e^{kt}$$

so that this function passes through the given points $(t_1, y_1)$ and $(t_2, y_2)$.

But, how do you find an exponential function from points?

Technically, in order to find the parameters you need to solve the following system of equations:

$$y_1 = A_0 e^{k t_1}$$ $$y_2 = A_0 e^{k t_2}$$

Solving this system for $A_0$ and $k$ will lead to a unique solution, provided that $t_1 = \not t_2$.

Indeed, by dividing both sides of the equations:

$$\displaystyle \frac{y_1}{y_2} = \frac{e^{k t_1}}{e^{k t_2}}$$ $$\displaystyle \Rightarrow \, \frac{y_1}{y_2} = e^{k (t_1-t_2)}$$ $$\displaystyle \Rightarrow \, \ln\left(\frac{y_1}{y_2}\right) = k (t_1-t_2)$$ $$\displaystyle \Rightarrow \, k = \frac{1}{t_1-t_2} \ln\left(\frac{y_1}{y_2}\right)$$

In order to solve for $A_0$ we notice from the first equation that:

$$A_0 = y_1 e^{-k t_1} = y_1 \frac{y_2}{y_1 e^{k t_2}} =\frac{y_2}{e^{k t_2}}$$

How do you calculate exponential growth?

It is not always growth. Indeed, if the parameter $k$ is positive, then we have exponential growth, but if the parameter $k$ is negative, then we have exponential decay.

The parameter $k$ will be zero only if $y_1 = y_2$ (the two points have the same height).

For specific exponential behaviors you can check our exponential growth calculator and the exponential decay calculator , which use specific parameters for that kinds of exponential behavior.