More about the uniform distribution probability

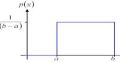
Here is a little bit of information about the uniform distribution probability so you can better use the the probability calculator presented above: The uniform distribution is a type of continuous probability distribution that can take random values on the the interval \([a, b]\), and it zero outside of this interval. The main properties of the uniform distribution are:

• It is continuous (and hence, the probability of any singleton event is zero)


• It is determined by two parameters: the lower (a) and upper (b) limits


• The population mean is \(\frac{a+b}{2}\), and the population standard deviation is \(\sqrt{\frac{(b-a)^2}{12}}\).

Using the above uniform distribution curve calculator , you will be able to compute probabilities of the form \(\Pr(a \le X \le b)\), with its respective uniform distribution graphs .

Type the lower and upper parameters a and b to graph the uniform distribution based on what your need to compute. If you need to compute \(\Pr(3 \le X \le 4)\), you will type "3" and "4" in the corresponding boxes of the script for the two-tailed test, for example.

Other common continuous probability distribution calculators that you can also use are the normal probability calculator , exponential probability calculator and the t-distribution calculator .