How to Use this x-intercept calculator with steps

This calculator will allow you to compute the x-intercept of a line, and you will get all the steps shown.

The x-intercept is the point where the line crosses the x-axis, if that ever happens.

In general, there is always an x-intercept when the slope is different from zero.

When the slope is zero, there will be an x-intercept only if the line also crosses the origin. Vertical lines also have an x-intercept.

How to find x intercept with steps with this calculator

All you need to do to use this calculator is to decide on one of the four options provided to define your line. Often times you will provide the slope and y-intercept, but also you can write down the equation of the line directly.

If the equation you provided is valid, the solver will go over the steps required to identify the x-intercept, or to indicate that no x-intercept could be found

Can you get the x-intercept from an line in standard form?

Yes! In fact, using the standard form of the line is one of the easiest ways to compute the x-intercept.

So, one common strategy is to first convert the equation of the line into standard form and then solve for \(x\) when \(y=0\).

Why do we need the x-intercept?

The x-intercept and y-intercept of a line have a great use to give a geometric intuition of the behavior on a line in the coordinate axes \(X - Y\).

Example of the calculation of the x-intercept given a line

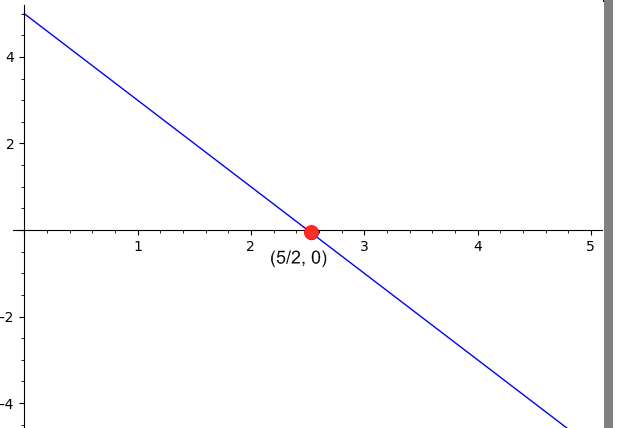
You know the standard form of the line \( \frac{3}{4} x + \frac{4}{5} y = 2\). Find the x-intercept of the line.

Answer:

We have been provided with the following equation:

\[\displaystyle 2x+y=y+5\]

So, who do you find x intercept: Passing all the variables and their coefficients to the left of the equation, and grouping the constants on the right, we get:

\[\displaystyle 2x+\left(1-1\right)y = 5\]

and simplifying all the terms that need simplification, we get that the equation in standard form is

\[\displaystyle 2x=5\]

The term \( y\) does not appear on the left hand side of the equation, so we can further solve for \( x\), which leads to

\[ 2 x = 5 \Rightarrow x=\frac{5}{2}\]

Observe that based on the above, this corresponds to a vertical line, that goes accross the value \(\displaystyle x=\frac{5}{2}\).

Conclusion: Based on the data provided, we conclude that the line crosses the x-axis at \(\displaystyle x = \frac{5}{2}\), hence, the corresponding x-intercept point is \(\displaystyle \left(\frac{5}{2}, 0\right)\).