Formula of Slope
Instructions: Use this calculator to compute the formula of slope, for any two points that you provide, showing all the steps. Please type in two points of the form (x, y) in the form box below.
More about the Formula of Slope
This slope formula calculator will allow you use compute the slope for two given points of the form (x, y) using the well known formula, showing all the steps.
You need to provide two points of the form (x, y). For example, you can provide points like (1/2, 1/3), or something that is not simplified like (1/3+1/4, sqrt(8)).
Once you provide two valid points of the form (x, y), the next step is to click on the button that says "Calculate" button, and you will be provided with all the steps of the slope formula calculations.
The concept of slope is a crucial one in Algebra and Geometry, and the slope is very important for the construction of a linear function.
What is the formula of slope?
Suppose we have two points \((x_1, y_1)\) and \((x_2, y_2)\) on the plane. Then the formula of slope is :
\[m = \displaystyle \frac{y_2 - y_1}{x_2 - x_1} \]Some people will say "it is the ratio between the difference in y's and the difference in x's", with the caveat that you need to preserve the order when doing the differences. If on top you do \(y_2 - y_1\), then at the bottom you do \(x_2 - x_1\) and not \(x_1 - x_2\).
Also, some people calls this slope formula "Rise versus Run"/
What are the steps for using the formula of slope
- Step 1: Identify the two given points. It is a good idea to simplify the expressions as much as possible, before using the formula
- Step 2: Determine which one is the first point, and what the second. The choice is irrelevant to the result, provided that you remain consistent with your choice
- Step 3: Use the formula \(b = \displaystyle \frac{y_2 - y_1}{x_2 - x_1}\) by plugging in the values of the first point \(x_1\) and \(y_1\), and of the second point \(x_2\) and \(y_2\)
- Step 4: After plugging the values in, simplify as much as possible, to reduce the slope to its simplest form
The calculation of the slope using the formula is usually a very simple process, just make sure to keep consistent the order of the points.
How to use the slope?
The slope is a measure of the inclination of a line. Indeed, when you have a linear function of the form
\[y = m x + n\]then, the slope of the line is m. The above is known as the slope-intercept form of a line.
What are the steps for using the slope for a line?
- Step 1: Identify the slope m. Simplify it as much as possible
- Step 2: You need to know the y-intercept, this is, the point in the y-axis when the line crosses it, and call it n
- Step 3: Then, the equation of the line is \(y = m x + n\)
There are other forms to express the line other than the slope intercept. You have the standard form of the line, and the point-slope form.
How to use the slope-intercept formula
That is the center of linear functions (or linear affine we should say) and linear graphs. Indeed, when you have the slope m and the y-intercept n, you directly compute the equation of the line as y = mx + n.
Geometrically, that is pretty simple to interpret, as the y-intercept is absolutely clear as the intersection point between the line and y-axis, and the slope is the measure of inclination. As a reference, a slope of m = 1 corresponds to an inclination of 45o.
Conversely, if you have any linear function, through algebraic simplification you can always reduce to the slope-intercept form y = mx + n, and then you have found your slope m and y-intercept n.

Example: Using the formula of slope
Calculate the slope for the following points: \(\displaystyle \left(\frac{1}{3}, \frac{5}{4}\right)\) and \(\displaystyle \left(\frac{7}{3}, \frac{7}{4}\right)\)
Solution: We need to compute the slope of a line that passes through the points \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) and \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\).
The following formula is needed to compute the slope given the two points:
\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]Now, plugging the values of the points \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) and \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) leads to:
Hence, we conclude that the slope of a line that passes through the points \(\displaystyle (x_1, y_1) = \left(\frac{1}{3},\frac{5}{4}\right)\) and \(\displaystyle (x_2, y_2) = \left(\frac{7}{3},\frac{7}{4}\right)\) is \(m = \displaystyle \frac{1}{4}\).
Example: More examples of the slope formula
Use the slope formula to find the slope of the line that passes through the points: \((2, 4)\) and \((5, 12)\)
Solution: In this case we have the points \(\displaystyle (x_1, y_1) = \left(2,4\right)\) and \(\displaystyle (x_2, y_2) = \left(5,12\right)\), which are the points we know the line passes through.
The slope formula is:
\[m = \displaystyle\frac{y_2-y_1}{x_2-x_1}\]Now, plugging the values of the points \(\displaystyle (x_1, y_1) = \left(2,4\right)\) and \(\displaystyle (x_2, y_2) = \left(5,12\right)\) leads to:
Hence, we conclude that the slope of a line that passes through the points \(\displaystyle (x_1, y_1) = \left(2,4\right)\) and \(\displaystyle (x_2, y_2) = \left(5,12\right)\) is \(m = \displaystyle \frac{8}{3}\).
Example: Slope-intercept form
Find the slope intercept form for the following line: \(2x + 4y = 3 + \frac{1}{2}x\).
Solution:We have the following equation:
\[\displaystyle 2x+4y=3+\frac{1}{2}x\]Putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get
\[\displaystyle 4y = \left(\frac{1}{2}-2\right)x +3\]Now, the term multiplying \(y\) is \( 4 - 0 = 4\), and also since \( \frac{1}{2} - 2 = -\frac{3}{2}\), the following is obtained
\[\displaystyle 4y=-\frac{3}{2}x+3\]Now, solving for \(y\), by dividing both sides of the equation by \(4\), the following is obtained
\[\displaystyle y=-\frac{\frac{3}{2}}{4}x+\frac{3}{4}\]and simplifying we finally get the following
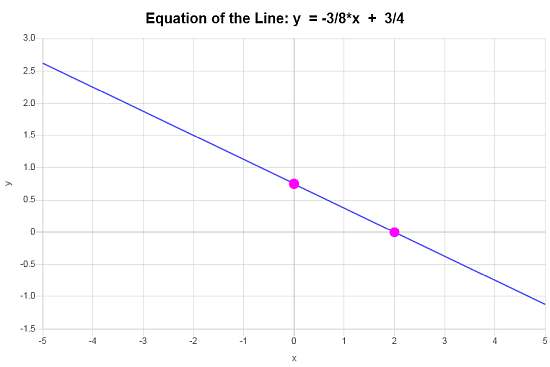
\[\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\]Conclusion: Based on the data provided, we conclude that the equation of the line in slope-intercept form is \(\displaystyle y=-\frac{3}{8}x+\frac{3}{4}\), with a slope of \(\displaystyle b = -\frac{3}{8}\) and y-intercept of \(\displaystyle n = \frac{3}{4}\).
Graphically, the line looks like:
Other linear function calculators
Together with quadratic functions, linear functions are among the most important objects in Math. you can compute the slope of a line, find the perpendicular line, and convert the line among different forms, depending on the needs.
One thing that is remarkable for linear functions, is that it is easier to find inverse linear functions, as most linear functions are 1-to-1 (except for horizontal lines).