More about Polynomial Inequalities

This calculator can help you with the solution of polynomial inequalities, by showing you all of the steps of the process of the calculation of the solution, plus providing you with a inequality graph, depicting the solution

The inequality you provide can be something simple like 'x^2 > 1', or it could be something more complex like 'x^3 + 3x^2 + 3x + 1 > 0'.

Once valid polynomial inequality is provided, please go ahead and click on the "Calculate" button, in order to get the solution and all the steps shown.

Please be aware that not all polynomials you provide will lend themselves to exact solutions. The lower the degree of the polynomial, the more likely that an exact solution to the inequality will be found.

What is a Polynomial Inequality

A polynomial inequality is a simply a type of inequality in which the expressions involved are polynomial, and none of its terms is a non-polynomial expression. For example

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \displaystyle \frac{x^3}{3} \]

is a polynomial inequality, whereas

\[\displaystyle \frac{1}{2} x^2 + \frac{3}{4} < \sin(x) \]

is a not, because of the presence of the term \(\sin x\), which is not a polynomial. Solving inequalities in general is a difficult process in general, but for polynomial ones, we have a clear plan of action.

How do you solve a polynomial inequality

• Step 1: Make sure all terms are polynomials. If not, the specific methods used for polynomials may not apply
• Step 2: Put everything on one side, leaving zero on the other side
• Step 3: Replacing the inequality sign by "=", solve the associated equation (this involves finding the zeros of a polynomial)
• Step 4: Collect all the critical points of the inequality, which in this case are the real zeros of the auxiliary polynomial equation (you don't consider the complex roots in this case)
• Step 5: If no critical points exist, it implies that the expression does not change sign, so the whole real line will be a solution, or no there is no solution. To check, choose any point and see if it satisfies the inequality, and if it does, the whole real line is the solution, if not, there is no solution
• Step 6: If there are critical points, construct intervals with consecutive critical poins (using -∞ as your starting critical point, and ∞ as your ending critical point)
• Step 7: Check each of those intervals, and see if a point inside meets the inequality. If it does, the interval is a part of the solution, if not, the interval is not a part of the solution.

The key idea here is that the critical points and the intervals we derive from them are intervals for which the expression does not change signs, so either the whole interval is a solution, or not point in the interval is part of the solution.

Polynomial Zeros and Critical Points

One of reasons why solving polynomial inequalities is possible is because it is relatively simple for polynomial expressions to be analyzed for critical points, aside from the fact that polynomials are continuous expressions.

There will be inequalities like

\[\displaystyle \frac{\sin(x^2-1)}{x^3-1} < 1 \]

in which it will be a lot harder to find critical points. Linear inequalities are even simpler to find critical points, but that is about it. Any general inequality will present its own complexities.

Applications of Polynomials in Real Life

There are plenty of applications of polynomials. For example, in Physics when you study Kinematics, there are some interesting polynomial expressions derived from Newton's Laws. This expressions can define conditions for the position of a body, which could lead to a polynomial inequality to determine which times the body is above certain height, which could prove crucial in ballistics, for example.

Also, when studying Differential Equations, you can find dumpering terms in the equation that depend on a power, and have polynomial structure, for which you can use some advanced inequalities, such as Gronwall's Inequalities.

Example: Solving Polynomial Inequalities

Solve: \(x^2 - x > \frac{1}{2}\)

Solution: We need to first solve the following given quadratic equation \(\displaystyle x^2-x-\frac{1}{2}=0\):

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(1\right)\left(-\frac{1}{2}\right)}}{2\cdot 1} = \displaystyle \frac{1 \pm \sqrt{3}}{2}\]

so then, we find that:

\[ {x}_1 = \frac{1}{2}-\frac{1}{2}\sqrt{3}=-\frac{1}{2}\sqrt{3}+\frac{1}{2} \] \[{x}_2 = \frac{1}{2}+\frac{1}{2}\sqrt{3}=\frac{1}{2}\sqrt{3}+\frac{1}{2}\]

Critical Points Analysis

The list of critical points found organized in ascending order is: \(-\frac{1}{2}\sqrt{3}+\frac{1}{2}\), \(\frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Based on this, we need to analyze the following intervals:

• For the interval \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): The left-hand side is positive, so then \(\left(-\infty, -\frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) is part of the solution.

• For the interval \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\): The left-hand side is negative, which means that \(\left(-\frac{1}{2}\sqrt{3}+\frac{1}{2}, \frac{1}{2}\sqrt{3}+\frac{1}{2}\right)\) is not a part of the solution.

• For the interval \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\): The left-hand side is positive, which means that \(\left(\frac{1}{2}\sqrt{3}+\frac{1}{2}, \infty\right)\) is part of the solution.

Solution to the Inequality

Based on the inequality provided, and analyzing the critical points, we find that the solution to the inequality is: \(x < -\frac{1}{2}\sqrt{3}+\frac{1}{2}\) or \(x > \frac{1}{2}\sqrt{3}+\frac{1}{2}\).

Using interval notation, the solution is written as:

\[\left(-\infty,-\frac{1}{2}\sqrt{3}+\frac{1}{2}\right) \cup \left(\frac{1}{2}\sqrt{3}+\frac{1}{2},\infty\right)\]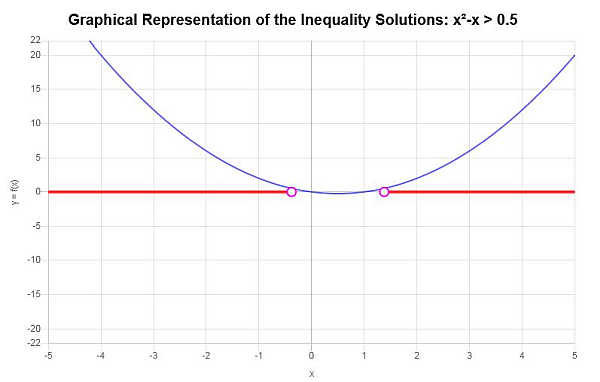

which concludes the calculation.

Example: Higher degree polynomial

Solve the following inequality: \(x^3 - x > 1\)

Solution:

In order to solve \(x^3-x > 1\) we first put everything on one side:

\[x^3-x-1> 0\]

Now, from this we obtain the associated equation that needs to be solved first, which is \(x^3-x-1=0\). Observe that the degree is \(\displaystyle deg(p) = 3\), its leading coefficient is \(\displaystyle a_{3} = 1\) and its constant coefficient is \(\displaystyle a_0 = -1\).

Attempting Rational Roots

We will try to find simple rational roots first, with the Rational Zero Theorem.

The next task is to find the integer numbers that divide the leading coefficient \(a_{3}\) and the constant coefficient \(a_0\), that will be used to construct our candidates to be zeroes of the polynomial equation.

▹ The dividers of \(a_{3} = 1\) are: \(\pm 1\).

▹ The dividers of \(a_0 = -1\) are: \(\pm 1\).

Therefore, dividing each divider of the constant coefficient \(a_0 = -1\) by each divider of the leading coefficient \(a_{3} = 1\), we find the following list of candidates to be roots:

\[\pm \frac{ 1}{ 1}\]

Now, all the candidates need to be tested to see if they are a solution. The following is obtained from testing each candidates:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -1^3-\left(-1\right)-1 & = & \displaystyle -1 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^3-1-1 & = & \displaystyle -1 \ne 0 \\\\ \end{array}\]

But since we have not found any rational roots by inspection, we cannot carry on with the factorization using elementary methods, so the process stops here.

OPTIONAL: This is a polynomial of degree \(3\), for which there are a total of \(3\) roots, even if some could be complex, but in this case less than \(3\) solutions have been found using elementary methods.

Using advanced cubic equation methods, it can be found that the complete set of solutions is:

\[x_1=\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\]
\[x_2=\frac{\frac{1}{6}\cdot \left(-3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}+i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]
\[x_3=\frac{\frac{1}{6}\cdot \left(3i\sqrt{3}\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-3\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{2}{3}}-i\sqrt{3}-1\right)}{\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}}\]

Critical Points Analysis

The only critical point that was found is \(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\).

Based on this, we need to analyze the following intervals:

• For the interval \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\): The left-hand side is negative, so then \(\left(-\infty, \left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}\right)\) is not a part of the solution.

• For the interval \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\): The left-hand side is positive, which implies that \(\left(\left(\frac{1}{18}\sqrt{23}\sqrt{3}+\frac{1}{2}\right)^{\frac{1}{3}}+\frac{1}{3}\left(-\frac{3}{2}\sqrt{23}\sqrt{3}+\frac{27}{2}\right)^{\frac{1}{3}}, \infty\right)\) is part of the solution.

Solution to the Inequality

Based on the inequality provided, and analyzing the critical points, we find that the solution to the inequality is: \(x > 1.3247180451128\).

Using interval notation, the solution is written as:

\[\left(1.3247180451128,\infty\right)\]

Graphically:

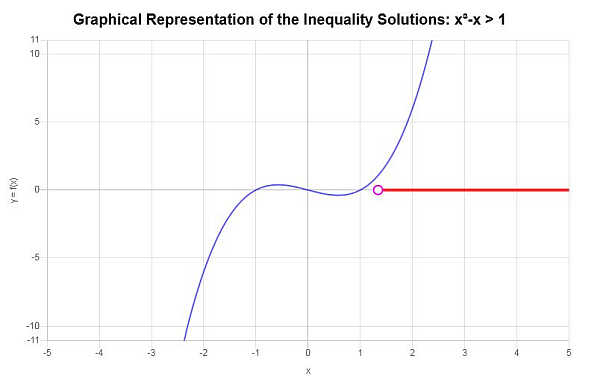
More Inequality Calculators

Solving inequalities (barred from finding solutions to equations) is one of the most common operations in Math, across the board.

The process of solving inequalities is usually laborious, and in general there is not a rule to solve them. Solving polynomial inequalities is one of the few exceptions, in which we can follow a set of steps to find the solutions, but yet, we can still fail, because higher degree polynomials are hard to deal. Indeed, it is really impossible to find polynomial roots above degree 5 using a general rule (Abel's Theorem).