What to know about this Binomial Expansion calculator

This binomial expansion calculator with steps will give you a clear show of how to compute the expression \[(a+b)^n\]

for given numbers \(a\), \(b\) and \(n\), where \(n\) is an integer. The above expression can be calculated in a sequence that is called the binomial expansion, and it has many applications in different fields of Math.

The Binomial Expansion of Order n

Using diverse approaches, the formula for a binomial expansion has been found, and it is as shown below

\[(a+b)^n = a^n + \dbinom{n}{1} a^{n-1} b + \dbinom{n}{1} a^{n-2} b^2 + ... \dbinom{n}{n-1} a b^{n-1} + b^n\]

where the term \(\dbinom{n}{k}\) computed is:

\[\dbinom{n}{k} = \frac{n!}{k! \times (n-k)!}\]

This term \(\dbinom{n}{k}\) is commonly known as the k^h binomial coefficient of a binomial expansion of order \(n\). As we can see, a binomial expansion of order \(n\) has \(n+1\) terms, when \(n\) is a positive integer.

Pascal's Triangle for a binomial expansion calculator negative power

One very clever and easy way to compute the coefficients of a binomial expansion is to use a triangle that starts with "1" at the top, then "1" and "1" at the second row. Then, from the third row and on take "1" and "1" at the beginning and end of the row, and the rest of coefficients can be found by adding the two elements above it, in the row immediately above, as shown in theceous chart below.

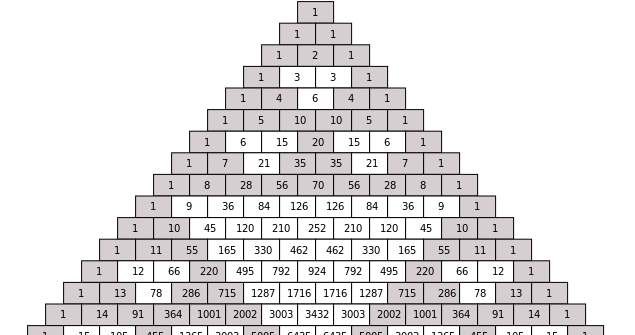
A Binomial expansion calculator negative powers

So far we have considered the order \(n\) to be a positive integer, but there is also an expansion when \(n\) is negative, only that is not necessarily finite, and it will involve an infinite number of terms in the general case.

Binomial Coefficients

Instead of computing the whole expansion, use this binomial coefficient calculator to get a specific term of the expansion.

Other interesting discrete distributions

The binomial distribution is not the only commonly used discrete distribution. We also have Poisson distribution, which is as much as commonly is as the binomial.

You can use this Poisson calculator to compute Poisson probabilities for any event of interest.