A System of Equations is simply a set of two or more simultaneous equations that the need to be solved. Typically, you will be have the same number of equations and unknowns (variables), but it does not have to be the case.

The only thing that is clear is that in order to have a system of equations you need to have TWO or MORE simultaneous equations. For example, the system below

is a system of equations, with two equations and two unknowns (\(x\) and \(y\)). Or for example, the system below:

is a system of equations, with two equations and three unknowns (\(x\), \(y\) and \(z\)).

The first example is an example of a system of linear equations.

The second example is an example of a system of non-linear equations. Why? You guessed it: the term \(z^2\) in the first equation makes it non-linear.

In general terms, the strategy used to solve a system of equations depends on whether it is linear or not. For linear systems of equations, there are systematic methods to solve them, such as Cramer's Rule . For non-linear systems of equations, there is not a fixed strategy and we need to go case by case.

Number of solutions of a system of equations

How many solutions does a system of equations have, if any? A general answer to this question only can be given with the case of systems of linear equations, based on the the relationship between the number of equations and the number of unknowns.

Typically, in a system of linear equations where the number of equations is the same as or greater than the number of unknowns, there could be a unique solution, no solution or infinite solutions.

When the number of equations is less than the number of unknowns, there could be an infinite number of solutions, or no solution at all, but there could not be a unique solution.

How do you find a system of equations?

This question is related to how do come across to a system of equations. There are several contexts. For example, you may be dealing with a word problem, in which you are producing three different types of foods, and you have a several types of restrictions on those foods in terms of cost, calories, etc. Each of those restrictions can probably be represented as an equation.

There are countless applications in which different restrictions lead to linear equations that need to be solved simultaneously, converting the problem into a system of equations.

EXAMPLE 1

System of equations example: It the following system of equations linear or non-linear?

ANSWER:

First of all, the above is a system of equations, with three equations and three unknowns (\(x\), \(y\) and \(z\)). The first two equations are linear whether the last equation is non-linear, because of the \(\sin(z)\) term. In order to have a linear equation, we need to have the unknowns to only be multiplied by a constant.

So, the above system of equations is not linear, even if the first two equations are linear, the third is not. For a system, it is enough to have one equation to not to be linear for the whole system to be non-linear.

EXAMPLE 2

Suppose that you product three types of shirts in the following amounts: \(x\), \(y\) and \(z\). Type 1 has cost of $1, type 2 a cost of $1.2 and type 3 a cost of $1.5. Also, it takes 1 hour to produce type 1, 0.5 hours to produce type 2 and 0.8 hours to product type 3.

I know that I have $800 to spend, and 500 hours available. Also, based on my demand estimates, I want to produce a total of type 1 shirts that is equation to the combined total of type 2 and type 3.

Write a system of equations based on these restrictions. Is this system linear?

ANSWER:

Notice that there are three unknowns (\(x\), \(y\) and \(z\)), which corresponds to the number of shirts of each type that need to be produced. Also, we have three equations: one for the cost, one for the number of hours available, and one for the restriction of the number of type 1 shirts and the other types.

The following equations represent the the situation:

Using the convention of leaving all the terms that depend on the unknowns on the left side, we rewrite the last equation to get:

Notice that each equation is linear, so then the system is a system of linear equations.

How do you solve systems of equalities in general?

As it was mentioned above, there is not a single strategy that would fit all the cases. Only in the case of linear systems of equation there will be a clear, well defined strategy.

Still, there are some good practices or steps that you have to follow that can help you solve all kinds of systems of equations:

Step 1: Identify each equation in the system

Step 2: Move to one side of the equation all the terms that depend on the unknowns (typically to the left side), and the constants on the other side

Step 3: Simplify both the left side (with the unknowns) and right side (with the constants)

Step 4: Identify the structure of the equations. Are the equations linear or non-linear?

Step 5: If all the equations are linear, use one of the systematic ways of solving linear systems (Cramer's rule, substitution, elimination, Gauss reduction, etc)

Step 6: If at least one equation is non-linear, you can try to use the substitution approach, starting by the simplest equation.

More About Systems of Equations

System of equations appear everywhere in Math, in all subjects. Being able to systematically solve systems of equations will prove to be a crucial skill to master.

The most typical system you will find is a system of linear equations. And frequently, you will find systems of equations that are linear, with two equations and two unknowns. These systems are usually call 2x2 system of linear equations.

System of Equations Graphing

For 2x2 system of linear equations, we have the benefit of being able to use a graphical representation in the coordinated axes. A linear equation is represented by a line in the x-y plane. Graphically, the solution of a 2x2 system is the point where the two lines intersect, if any.

Then, in this case we have that either: the lines are parallel and don't touch each other (no solutions), the lines intersect in one point (unique solution), or the lines are parallel and touch each other (infinitely many solutions)

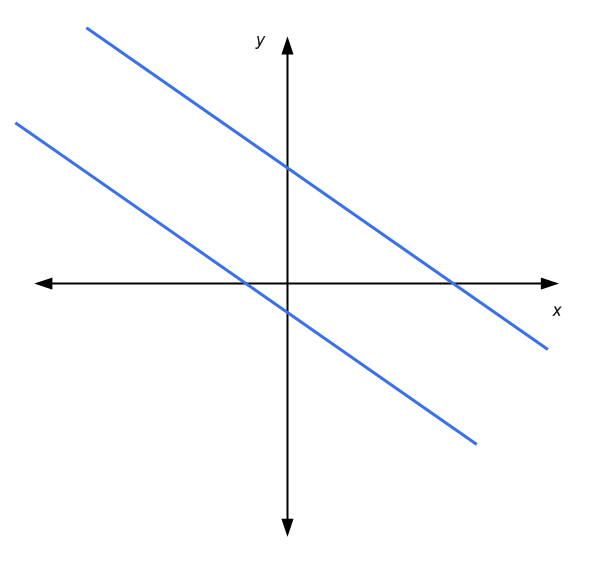
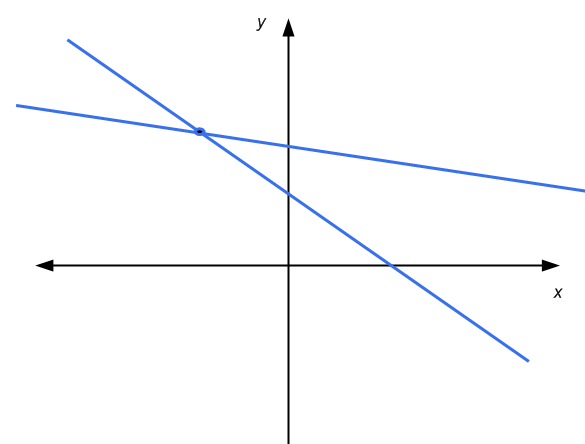
System of equations Calculator

Use this solver if you want to solve a 2x2 system of linear equations . This calculator uses Cramer's rule to solve 2x2 systems. For larger systems of equations, the best alternative is to use the Gaussian elimination method , which systematically deals with linear systems of any size.