How to use this Pythagorean Theorem Calculator

1. You have three boxes where you can input data
2. The forms represent sides a and b, and the hypotenuse c
3. Please type in the values of TWO of those boxes
4. For example, if you know that the sides are a = 3 and b = 4, then you type 3 in the first form, and 4 in the second box
5. Or, for example, if you know that the hypotenuse is c = 10/3 and side a is 5, then you type 5 in the first form, and 10/3 in the third box and leave the second box empty

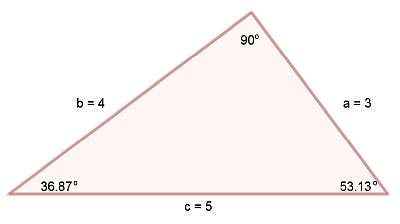
Pythagoras Theorem Formula

The basic Pythagoras formula is

\[\large a^2 + b^2 = c^2\]

and this formula is telling you how to find "c" if you know "a" and "b".

But also, you could find "a" if you know "c" and "b", and you could solve "b" if you know "c" and "a".

How do you solve right triangles

This Pythagorean Theorem Calculator will show you all the steps of the calculation of Pythagorean theorem formula.

This is not only a hypotenuse calculator, as you can also provide one side and the hypotenuse, and the calculator will show you all the steps to get the other side.

The most typical application is that where you have two sides in a right triangle, and you want to get the hypotenuse. But ultimately, the idea in a right triangle is that if you two sides (in general), you can get the third side using one version of Pythagoras' formula.

So with two pieces of information, you can find the length of the missing side.

Is this a right triangle calculator only

Yes, it is. This calculator only deals with right triangles. If your triangle is not right, you can use this SAS triangle calculator (where you provide two sides and one angle, which could be any angle, not necessarily 90^o.), this SSS triangle calculator (where you know the three sides and you want to find all the angles).

Or, you could this AAS triangle calculator (where you know two angles and the opposite side).

How do you calculate Pythagorean theorem?

Step 1: First, you need to assess what information you have. Do you have the two sides a and b, and you are looking for the hypothenuse c? Or do you know c and a, or c and b?

Step 2: If you know the two sides a and b, this hypotenuse calculator will get the hypotenuse using the following formula

\[c = \sqrt{a^2 + b^2}\]

and that is how you find the hypotenuse.

Step 3: If you know the one side and the hypotenuse, so say you know a and c, now the calculator will get the other side, b, using the following formula

\[b = \sqrt{c^2 - b^2}\]

The angle of the Pythagorean theorem calculator

This calculator requires one of the angles to be 90^o in order for the Pythagorean formula to be valid.

Can you use Pythagoras for angles? No, notice that this Pythagorean calculator only deals with sides, and it does not calculate angles.

If you want to completely solve a triangle (solving a triangle means finding sides and angles), you can use these: SAS triangle calculator , SSS triangle calculator and AAS triangle calculator.

Example of the calculation of a right triangle

Question: Assume that the sides of a right triangle are a = 3 and b = 3. Use Pythagoras Theorem to compute the hypothenuse c.

Solution: We have been provided with two sides, \(a =\displaystyle3\) and \(b = \displaystyle 6\). We need to use the Pythagorean formula to compute the hypothenuse \(c\).

Based on this information, the following Pythagorean formula needs to be used:

\[c = \displaystyle\sqrt{a^2 + b^2}\]

So now, plugging the values that we have available, the following is obtained:

\[c = \displaystyle\sqrt{a^2 + b^2} = \displaystyle\sqrt{3^2 + 6^2} = \displaystyle\sqrt{9 + 36} = \displaystyle\sqrt{45} = 3\sqrt{5}\]

Therefore, and summarizing, we have found that \(a = 3\), \(b = 6\) and \(c = 3\sqrt{5}\).