How to Compute Regression Residuals

Regression residuals correspond to the difference between the observed values (\(y\)) and the corresponding predicted values (\(\hat y\)).

Regression residual equation

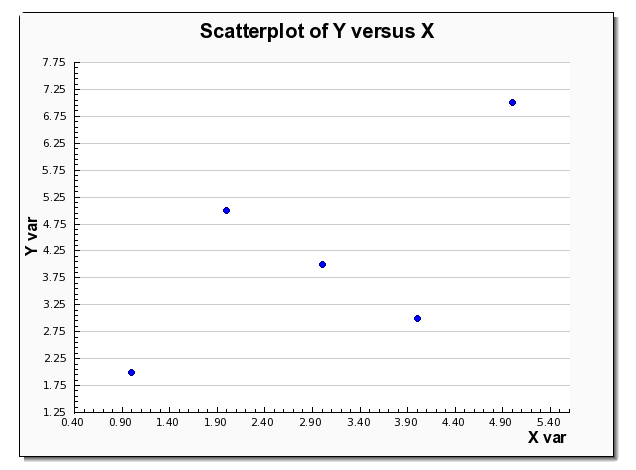
When conducting a linear regression analysis, the first step is to make a scatterplot of the data for X and Y that you have available, and if a relatively tight linear pattern is observed, you then can validly conduct the linear analysis

Let us recall that if \(\hat \beta_0\) and \(\hat \beta_1\) are the corresponding estimated y-intercept and slope, respectively, then the predicted value (\(\hat y\)) for a given value \(x\) is

\[ \hat y = \hat \beta_0 + \hat \beta_1 x \]

Then, the residual associated to the pair \((x,y)\) is defined using the following residual statistics equation:

\[ \text{Residual} = y - \hat y \]

The residual represent how far the prediction is from the actual observed value. This means that we would like to have as small as possible residuals.

Indeed, the idea behind least squares linear regression is to find the regression parameters based on those who will minimize the sum of squared residuals.

How to find the residuals for a regression

• Collect the sample data for X and Y
• Conduct a linear regression analysis and find the regression equation \(\hat y = \hat \beta_0 + \hat \beta_1 x\)
• For each sample point \(x_i\) and \(y_i\) you compute the residual using the formula: \(\text{Residual} = y_i - \hat y_i \)
• Once you have all the residual points, you can plot them in different ways to assess the quality and properties of the model estimated
• Calculating residuals is important because it provides a graphical way of assessing the plausibility of regression assumptions.
• In order for the regression results to be reliable, you expect residuals to have at least a normal probability distribution .

What does This Residual Calculator do?

What this residual calculator will do is to take the data you have provided for X and Y and it will calculate the linear regression model, step-by-step.

Then, for each value of the sample data, the corresponding predicted value will calculated, and this value will be subtracted from the observed values y, to get the residuals.

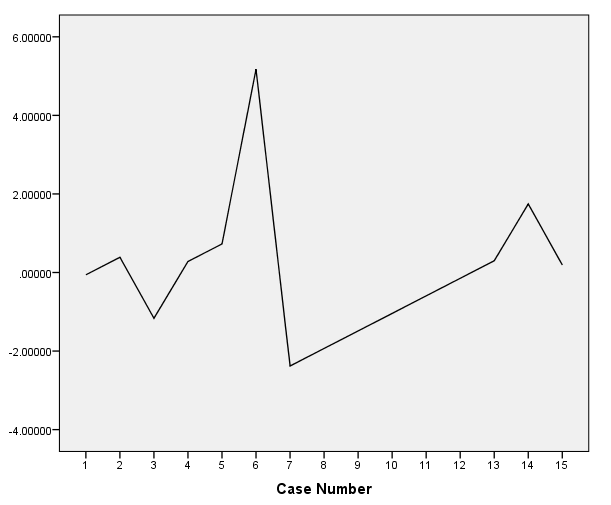
All of this will be tabulated and neatly presented to you. Also, a scatterplot of residuals versus predicted values will be presented. This residual plot is crucial to assess whether or not the linear regression model assumptions are met.

What else can you do with these data

Usually, one initial step in conducting a linear regression analysis is to conduct a correlational analysis. You can use our correlation coefficient calculator to find the correlation coefficient, that indicates the degree of association between the two variables.

The calculation of the correlation coefficient usually goes along with the construction of a scatter plot. Using a scatterplot and the correlation coefficient we can decide whether or not it is appropriate to conduct a linear regression analysis, especially if we found out using this correlation coefficient significance calculator , that the correlation is significantly different from zero.