Line Point-Slope Form Calculator
Instructions: Use this calculator to find the slope-intercept form of the line you provide, with all the steps shown. To that end, you need to give some information about the line that you want to put in point-slope form.
There are several different ways you can tell us about your line. You can provide: (1) both the slope and the y-intercept, (2) you can type in any linear equation (ex: \(x + 3y = 2 + \frac{2}{3}x\)), (3) you can indicate the slope and a point that the line passes through, or (4) you can indicate two points where the line passes through.
About this point-slope form calculator of the line.
This point-slope equation calculator will provide you a step-by-step calculation of the equation of the line in point-slope form for any line that you have initially provided.
What you need to do is to identify the line you want to work with. This line can be identified in many different and you will select based on what information you have provided.
One of the most common ways is to define a line by providing its slope and its y-intercept, but it is certainly not the only way.
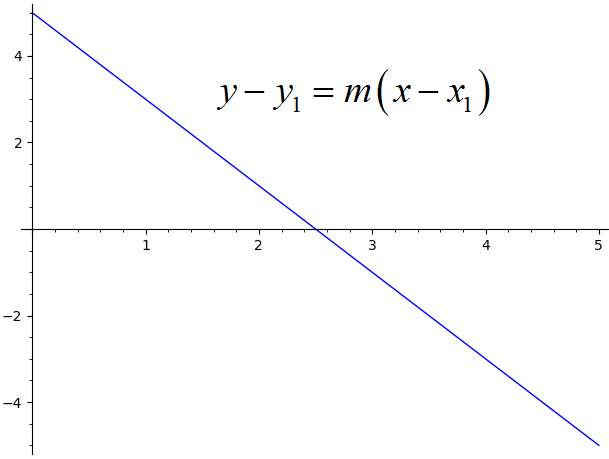
How to represent a line in point-slope form?
A line is said to be in point-slope form if it can be written as:
\[y - y_1= m (x -x_1)\]In this context, \(m\) is identified as the slope of the line, and \((x_1, y_1)\) is a point the line passes through.
How can you find the point-intercept with a calculator?
If you happen to know the slope \(m\) of the line and a point \((x_1, y_1)\) where the line passed through, then process is easy and direct, but it could be trickier if you have the line defined using other kind of information.
Why is the point-slope form of a line useful
The point-slope form is useful because it gives as a direct interpretation of the slope of the line as the rate of change. Indeed, directly from the point-slope form we get
\[\frac{y-y_1}{x-x_1} = m\]Can I get Point slope form with two points?
Yes! If you have two points, you use them first to compute the slope \(m\), and the choose any of the points to apply directly the formula
\[y - y_1= m (x -x_1)\]
Example: Point-Slope form calculation
Assume that you know that the line passes through the points \(( \frac{1}{3}, 2)\) and \((\frac{7}{2}, 3)\). Find the point-slope form of the line.
Answer:
The information provided about the line is that the line passes through the points\(\displaystyle \left( \frac{1}{3}, 2\right)\) and \(\displaystyle \left( \frac{7}{2}, 3\right)\)
Therefore, the first step consists in computing the slope. The formula for the slope is: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} \]
Now, by plugging the corresponding numbers is , we get that the slope is: \[\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{ \displaystyle 3 - 2}{ \displaystyle \frac{7}{2} - \frac{1}{3}} = \frac{ \displaystyle 1}{ \displaystyle \frac{19}{6}} = \frac{6}{19}\]
So then, now we know that the slope is \(\displaystyle m = \frac{6}{19}\) and that the line passes through the point \(\displaystyle \left( \frac{1}{3}, 2\right)\)
Hence, with the information we have, we can construct directly the point-slope form of the line, which is
\[\displaystyle y - y_1 = m \left(x - x_1\right)\]and then plugging the known values of \(\displaystyle m = \frac{6}{19}\) and \(\displaystyle \left( x_1, y_1 \right) = \left( \frac{1}{3}, 2\right)\), we get that
\[\displaystyle y-2 = \frac{6}{19} \left(x-\frac{1}{3}\right)\]Conclusion: Based on the data provided, we conclude that the equation of the line in point-slope form is \(\displaystyle y-2=\frac{6}{19}\left(x-\frac{1}{3}\right) \).
You can also use our standard form calculator and slope-interpcept calculator of a line, if those are instead the formats you are interested in.