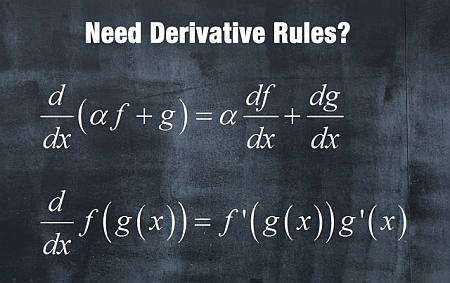About Derivative Rules
This calculator will allow you compute the derivative of a function you provide by applying the required basic
differentiation rules, showing all the steps of the process, and noting where each rule is applied.
You just need to provide a valid function that is differentiable (which means that it has a derivative). For
example, a valid function could be f(x) = 1/3*x*sin(x), just to mention one example.
Then, when you have already typed your function, you just click on "Calculate" to get all the steps of the differentiation shown.
The simplicity of the rules of derivatives makes the process of differentiation one that is recognized as 'easy', a judgment that is perhaps an overstatement.
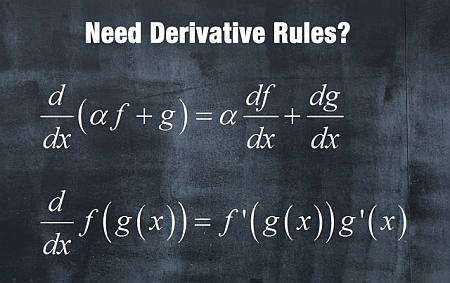
Basic derivative rules
There are four basic derivative rules for you to learn
- Linearity Rule: For functions \(f(x)\) and \(g(x)\), and a constant \(a\), then the derivative is a linear operation: \((af(x)+g(x))' = af'(x)+g'(x)\)
- Product Rule For functions \(f(x)\) and \(g(x)\), the derivative of the product is \((f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\)
- Quotient Rule: For functions \(f(x)\) and \(g(x)\), the derivative of the quotient is is \(\left(\frac{f(x)}{g(x)}\right)' = \left(\frac{f'(x)g(x) - f(x)g'(x)}{g^2(x)}\right)\)
- Chain Rule For functions \(f(x)\) and \(g(x)\), the derivative of the composite function is \((f(g(x)))' = f'(g(x))g'(x)\)
This rules will work like a charm and will help you find the derivative of any basic function.
How to use the derivative rules?
- Step 1: Identify the function f(x) you want to differentiate, simplify if needed
- Step 2: Try to break the function into smaller derivative chunks, using linearity
- Step 3: Depending on the structure of the function f(x), use any of the available rules (product, quotient and chain rule), and
be aware that you may need to apply many of the rules consecutively)
Usually you will end up a combination of several differentiation rules, until you reach of point where you find an elementary function, of which you
already know how to differentiate.

Can I solve all derivatives
Saying that using differentiation rules can lead you to solving ALL derivatives can be an overstatement. You will be able to solve MOST derivatives, and
certainly all basic ones, but there are functions that have a less intuitive behavior that could be defined, though they are no typically dealt with in
basic Calculus courses.
For what basic functions are concerned, most of them will be differentiated without a problem.
A product rule derivative, quotient rule derivative or chain rule derivative
are unlikely to be in isolation,
and will likely come in a sequence of several rules that need to be used together.

Example: Derivative Rules
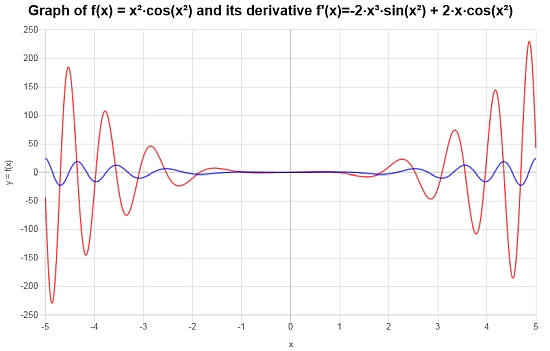
Using basic derivative rules, compute the following derivative: \(\frac{d}{dx}\left( x^2 \cos(x^2) \right)\)
Solution:Let us consider the following given function for which the derivative needs to be computed
\(\displaystyle f(x)=x^2\cos\left(x^2\right)\)
The function does not need simplification, so we can go straight into computing its derivative:
\( \displaystyle \frac{d}{dx}\left(x^2\cos\left(x^2\right)\right)\)
Now, using the Product Rule: \(\frac{d}{dx}\left( x^2\cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x^2\right) \cdot \cos\left(x^2\right)+x^2 \cdot \frac{d}{dx}\left(\cos\left(x^2\right)\right)\)
We have to use the Chain Rule: \(\frac{d}{dx}\left( \cos\left(x^2\right) \right) = \frac{d}{dx}\left(x^2\right)\cdot \left(-\sin\left(x^2\right)\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x\right) \cos\left(x^2\right)+x^2 \cdot 2x\cdot \left(-\sin\left(x^2\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle x^2\cdot 2x\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)
By reordering some of the numerical values, and then grouping the terms with \(x\) in the term \(x^2\cdot 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle 2x^3\cdot \left(-\sin\left(x^2\right)\right)+2x\cos\left(x^2\right)\)
But we get \((2x^3) \cdot (-\sin\left(x^2\right)) = -2x^3\sin\left(x^2\right) = -2x^3\sin\left(x^2\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle -2x^3\sin\left(x^2\right)+2x\cos\left(x^2\right)\)
And finally, grouping the terms together
\( \displaystyle = \,\,\)
\(\displaystyle -2\left(x^2\sin\left(x^2\right)-\cos\left(x^2\right)\right)x\)
The corresponding graph of the function and its derivative is shown below:
Example: More derivative rules
Compute the following derivative: \(\frac{d}{dx}\left( x \cos(x^2+1) \right)\) using basic derivative rules.
Solution:Now, the task at hand is to differentiate the function
\(\displaystyle f(x)=x\cos\left(x^2+1\right)\)
\( \displaystyle \frac{d}{dx}\left(x\cos\left(x^2+1\right)\right)\)
In this case, we have to use the Product Rule: \(\frac{d}{dx}\left( x\cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(\cos\left(x^2+1\right)\right)\)
The Chain Rule for this composition: \(\frac{d}{dx}\left( \cos\left(x^2+1\right) \right) = \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \cdot \frac{d}{dx}\left(x^2+1\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
By linearity, we know \(\frac{d}{dx}\left( x^2+1 \right) = \frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(1\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
The derivative of a constant is 0, so then:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(\frac{d}{dx}\left(x^2\right)\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \cos\left(x^2+1\right)+x \left(2x\right)\cdot \left(-\sin\left(x^2+1\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle x\cdot 2x\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)
Putting together the numerical values and grouping the terms with \(x\) in the term \(x\cdot 2x\)
\( \displaystyle = \,\,\)
\(\displaystyle 2x^2\cdot \left(-\sin\left(x^2+1\right)\right)+\cos\left(x^2+1\right)\)
Observe that \((2x^2) \cdot (-\sin\left(x^2+1\right)) = -2x^2\sin\left(x^2+1\right) = -2x^2\sin\left(x^2+1\right)\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle -2x^2\sin\left(x^2+1\right)+\cos\left(x^2+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle -2x^2\cos\left(x^2\right)\sin\left(1\right)-2x^2\cos\left(1\right)\sin\left(x^2\right)+\cos\left(1\right)\cdot \cos\left(x^2\right)-\sin\left(1\right)\cdot \sin\left(x^2\right)\)
Example of derivative rules
For the function \( f(x) = (x-1)(x^2+1) \), use derivative rules to find its derivative.
Solution: For this final example, we need to differentiate: \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\).
Initial Step: In this case, we first need to expand the given function \(\displaystyle f(x)=\left(x-1\right)\left(x^2+1\right) \), and in order to do so, we conduct the following simplification steps:
\( \displaystyle f(x)=\left(x-1\right)\left(x^2+1\right)\)
Note that \((x-1) \cdot (x^2+1) = x\cdot x^2+x-x^2-1^2 = x^3-x^2+x-1\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle x^3-x^2+x-1\)
After expanding the function, we can proceed to the calculation of the derivative:
\( \displaystyle \frac{d}{dx}\left(x^3-x^2+x-1\right)\)
By linearity, we know \(\frac{d}{dx}\left( x^3-x^2+x-1 \right) = \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\)
The derivative of a constant is 0, so then:
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+\frac{d}{dx}\left(x\right)\)
We know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x^3\right)-\frac{d}{dx}\left(x^2\right)+1\)
Using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\) and \(\frac{d}{dx}\left( x^3 \right) = 3x^2\)
\( \displaystyle = \,\,\)
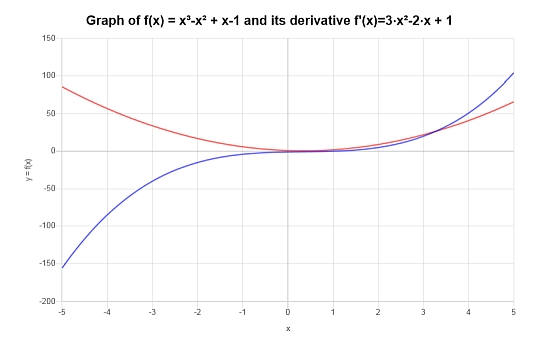
\(\displaystyle 3x^2-2x+1\)
Graphically, this is how the function and its derivative look:
More derivative calculators
One of the magic things about differentiation is that you can find the derivative of any function using some basic and simple rules,
including the product rule, quotient rule and naturally, the chain rule.
This small arsenal is usually sufficient to compute any derivative you need
Differentiation and integration are the main lanes in Calculus, without any dispute, as they are the center of so many applications,
in all aspects of science. From related rates to implicit differentiation, with
partial derivatives in Physics and Economics