How to use the Critical T-values Calculator

More information about critical values for the t-distribution : First of all, critical values are points at the tail(s) of a specific distribution, with the property that the area under the curve for those critical points in the tails is equal to the given value of \(\alpha\)

The distribution in this case is the T-Student distribution. In general terms, for a two-tailed case, the critical values correspond to two points to the left and right of the center of the distribution, that have the property that the sum of the area under the curve for the left tail (from the left critical point) and the area under the curve for the right tail is equal to the given significance level \(\alpha\).

Critical t-values

For a left-tailed case, the critical value corresponds to the point to the left of the center of the distribution, with the property that the area under the curve for the left tail (from the critical point to the left) is equal to the given significance level \(\alpha\).

For a right-tailed case, the critical value corresponds to the point to the right of the center of the distribution, with the property that the area under the curve for the right tail (from the critical point to the right) is equal to the given significance level \(\alpha\).

What Are the Main Properties of the T-distribution?

The main properties of the T-distribution and its critical points are:

• The t-distribution is a symmetric, continuous distribution, that is determined by the number of degrees of freedom (df)


• The t-distribution converges (in a distributional sense) to the standard normal distribution (Z-distribution) as the degrees of freedom (df) converge to infinity


• The t-distribution is used for various t-tests, where the population standard deviation is not known


• Since the t-distribution is symmetric, the critical points for the two-tailed case are symmetric with respect to the center of the distribution


• Also, since the t-distribution is symmetric, finding critical values for a two-tailed test with a significance of \(\alpha\) is the same as finding one-tailed critical values for a significance of \(\alpha\)/2

The t-distribution is the underlying distribution used for the very commonly used in statistical applications t-test for paired samples and t-test for two independent samples. These tests are crucial to assess statistical significance of the differences, for paired and non-paired data.

Do I need a t-critical value table?

Technically you can use a t critical value table, which you can find in the back of your Stats 101 book, but using this critical t-value calculator will eliminate that need. When working with statistical tables, you will need to locate the right table and position for the corresponding number of degrees of freedom and alpha level.

In the case of our calculator, you provide degrees of freedom and alpha level, and press a button. Then you get the requested t-critical value as well as the t-distribution graph showing the correct tail(s) associated to the critical value(s).

Example: Critical t-value calculation example

What is the t-critical value for alpha = 0.01, for a two-tailed test, with a sample size of n = 31?

Solution: First, the number of degrees of freedom is df = n - 1 = 31 - 1 = 30. Hence, for a two-tailed test, we need to find the value on the t-distribution with 30 degrees of freedom that has a probability of 0.01/2 = 0.005 on the right tail.

Hence, the critical t-value is \(t_c = 2.750\). Since this is a two-tailed test, we have that the critical values are \(t_c = \pm 2.750\).

Graphically:

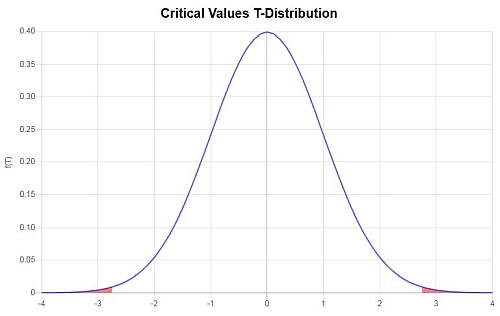
Also, the rejection region associated is \(R = \{t: |t| > 2.750\}\)

Other Critical Value Calculators

This one is for finding t values. We have many other critical values calculators, such as the z-critical values calculator , F-critical values calculator , and the Chi-Square critical value calculator .

Using critical values is one of the most common approaches to test statistical hypotheses, by comparing the values of obtained by a test value calculator with the corresponding critical values, as indeed the critical values are directly used to construct rejection regions.