Learn more about this perpendicular line calculator.

Lines are in big part determined by their slope (inclination). Horizontal lines are lines with slope equal to zero, an vertical lines are lines where the slope is undefined (negative or positive infinity).

Perpendicular lines are lines that cross forming a right angle. There is a specific condition for the slope and the perpendicular slope, whenever the slopes are defined, for the lines to be perpendicular, which is that the product of the slopes is -1.

Observe that one given line has infinite perpendicular lines to it. In order to find that one you are looking for, you need to fix a point it passes through.

How do you find the perpendicular line of a line?

The strategy is simple. The step is to find the slope of the given line. If you are provided with the slope and intercept to define the line then you already have the slope.

Otherwise, perhaps you have two points where the line passes through, in which case you can compute the slope directly.

Ultimately, if you define your given line with an equation, you need to get that equation into the slope-intercept form, so to get the slope.

Once you have the slope of the given line, you use the formula for the perpendicular slope, by multiplying by minus one the reciprocal of the original slope.

What is the perpendicular line of a horizontal line

The perpendicular line to a horizontal line is a vertical line.

What is the perpendicular line of a vertical line

The perpendicular line to a vertical line is a horizontal line.

Can you calculate the perpendicular line with no points

Once you have a line, there is not one but many (infinite) perpendicular lines to the given line. In order to identify one specific perpendicular line, you need to provide one point where the line passes through.

Typically, you will provide a point on the original line, where you want the perpendicular line to pass through.

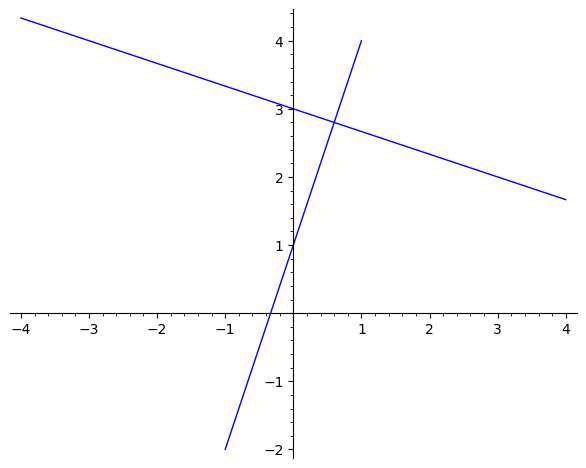
Example of the calculation of a perpendicular line for a given line:

Consider the line with equation \(2x + 3y = 5)\). Find the equation of the perpendicular line that passes through \((1, 1)\).

Solution: We first get the slope intercept equation for the GIVEN line, if possible

We have been provided with the following equation:

\[\displaystyle 2x+3y=5\]

Putting \(y\) on the left hand side and \(x\) and the constant on the right hand side we get

\[\displaystyle 3y = -2x +5\]

Then, solving for \(y\), by dividing both sides of the equation by \(3\), the following is obtained

\[\displaystyle y=-\frac{2}{3}x+\frac{5}{3}\]

Perpendicular Slope Formula

In general, the formula needed to compute the perpendicular slope, \(m_{\perp}\), is:

\[m_{\perp} = \displaystyle -\frac{1}{m}\]

By plugging the value of \(m = \) in the formula, we find that the perpendicular slope is

\[m_{\perp} = \displaystyle -\frac{1}{m} = \displaystyle -\frac{1}{} = \frac{3}{2}\]

Perpendicular Line Construction

Now, we have calculated that the perpendicular slope is \(m_{\perp} = \frac{3}{2}\) the and we know that the perpendicular line passes through the point \((1, 1)\).

Hence, with the information we have, we can construct directly the point-slope form of the line, which is

\[\displaystyle y - y_1 = m_{\perp} \left(x - x_1\right)\]

and then plugging the known values of \(\displaystyle m_{\perp} = \frac{3}{2}\) and \(\displaystyle \left( x_1, y_1 \right) = \left( 1, 1\right)\), we get that

\[\displaystyle y-1 = \frac{3}{2} \left(x-1\right)\]

Now, we need to expand the right hand side of the equation by distributing the slope, so we get \[\displaystyle y = \frac{3}{2} x + \frac{3}{2} \left(-1\right) + 1\]

and simplifying we get that \[\displaystyle y=\frac{3}{2}x-\frac{1}{2}\]

Therefore, we conclude that the equation of the given line is \(\displaystyle y=-\frac{2}{3}x+\frac{5}{3}\) and the equation of the perpendicular line is \(\displaystyle y=\frac{3}{2}x-\frac{1}{2}\).

If you want to make things more direct, use this perpendicular slope calculator and use the perpendicular line formula to get directly the slope of the line that is perpendicular line.

That is for the case that you only are looking for the slope in the context of what you are doing.