More about Quadratic Inequalities

This quadratic inequality calculate will provide you with solutions to inequalities showing all the steps. For example, the inequality you provide can something like 'x^2 - 1/2 > 0', and in general, quadratic inequalities do not get too hard to solve.

Once you provide a valid inequality involving quadratic expression, you can click on "Calculate" to get all the steps of the calculation shown to you, including a graph of the inequality solutions.

Quadratic inequalities are one of the few types (along with linear inequalities) that you are guaranteed to be able to find an exact solution, and this process involves solving a quadratic equation.

What is the definition of this type of inequality

We haven't stated it explicitly, but it comes sort of clear from its name: a quadratic inequality is a specific type of inequality in which all the terms involved in it are polynomials of at most degree 2. In this context, one example is

\[\displaystyle x^2 < x - 1\]

which is quadratic by the fact that both sides of the inequality are polynomials of order at most 2. Now, if you had:

\[\displaystyle x^2 < x^3 - 1\]

then the inequality is not quadratic any longer, because of the term \(x^3\) on the right hand side. For these inequalities we have a clear roadmap to find the solution.

Steps for Solving Inequalities that are Quadratic

• Step 1: Make sure that you have a quadratic inequality, as the method used in this case is valid only for this type of inequality
• Step 2: As with most inequalities, pass everything to the left side of the inequality, and solve the associated equation
• Step 3: If the associated quadratic equation does not have real roots, we then know that either the whole real line is a solution, or there is no solution. So you test any point and see if it solves the inequality, and if it does, the solution is the whole real line (-∞, ∞), otherwise, the solution is empty.
• Step 4: If the associated quadratic equation has only one real solution, it means that associated quadratic graph touches tangentially the x-axis. So depending on the inequality sign, you may have only the touching point being the solution, or everything except the touching point being the solution, or the whole real line (-∞, ∞), for which you need to test the touching point, and a point outside of that (to the left and right of the point)
• Step 4: If the associated quadratic equation has two different real solutions, you check intervals defined by these roots to determine which portions of the real line will be a part of the solution

One you analyze the pieces, if needed, you join them by using the "union" operator, which is used to piece intervals together.

How do you draw a quadratic inequality?

Graphing inequalities provides a great way of visually understanding how the solution looks like. In terms of the procedure, you need to know whether you are working with a one variable inequality, or you have more variables.

If you have an inequality such as

\[\displaystyle x^2 - \frac{1}{2} x < 1 \]

you have only one variable, and then the solution will be a subset of the real line. On the other hand, if you had something like

\[\displaystyle y < x^2 - \frac{1}{2} x \]

then you have only two variables x and y, and then the solution of the inequality wiil be a subset of the x-y plane.

Importance of Quadratic Expressions

Quadratic expressions involved in equations and inequalities play a fundamental role in Mathematics. Perhaps, quadratic is the most broadly used type of structure after linear.

When dealing with Calculus and Algebra you will find countless applications of quadratics in problems of maximization and minimization, integration, and a lot more. Digging a bit you will find applications of quadratic expressions all over different scientific displines

Example: Quadratic Inequalities

Solve this quadratic inequality: \(\frac{1}{3}x^2 + \frac{5}{4}x - \frac{5}{6} < 0\)

Solution:

We need to first solve the following auxiliary quadratic equation \(\displaystyle \frac{1}{3}x^2+\frac{5}{4}x-\frac{5}{6}=0\).

Applying the Quadratic Formula

The quadratic equation is:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In this case, we have:

\[a = \frac{1}{3}\] \[b = \frac{5}{4}\] \[c = -\frac{5}{6}\]

Plugging these values into the formula for the roots we get:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\left(\frac{5}{4}\right)^2-4\left(\frac{1}{3}\right)\left(-\frac{5}{6}\right)}}{2\cdot \frac{1}{3}} = \displaystyle \frac{-\frac{5}{4} \pm \sqrt{\frac{385}{144}}}{\frac{2}{3}}\]

so then, we find that:

\[ {x}_1 = -\frac{\frac{5}{4}}{\frac{2}{3}}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}-\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{1}{8}\sqrt{385}-\frac{15}{8} \] \[{x}_2 = -\frac{\frac{5}{4}}{\frac{2}{3}}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{-5\cdot 3}{4\cdot 2}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=-\frac{15}{8}+\frac{1}{\frac{2}{3}}\sqrt{\frac{385}{144}}=\frac{1}{8}\sqrt{385}-\frac{15}{8}\]

Critical Points

The list of critical points found organized in ascending order is: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}\), \(\frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Then, we need to analyze the following critical intervals:

• For the interval \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): The left-hand side is positive, so then \(\left(-\infty, -\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) is not a part of the solution.

• For the interval \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\): The left-hand side is negative, which implies that \(\left(-\frac{1}{8}\sqrt{385}-\frac{15}{8}, \frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\) is a part of the solution.

• For the interval \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\): The left-hand side is positive, which means that \(\left(\frac{1}{8}\sqrt{385}-\frac{15}{8}, \infty\right)\) is not a part of the solution.

Solution

Based on the inequality provided, and analyzing the critical points, we find that the solution to the inequality is: \(-\frac{1}{8}\sqrt{385}-\frac{15}{8}< x \le \frac{1}{8}\sqrt{385}-\frac{15}{8}\).

Using interval notation, the solution is written as:

\[\left[-\frac{1}{8}\sqrt{385}-\frac{15}{8},\frac{1}{8}\sqrt{385}-\frac{15}{8}\right)\]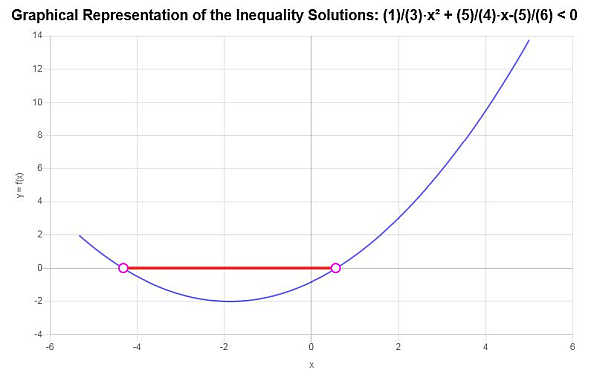

Example: More Quadratic Inequalities

Solve: \(x^2 < 4\)

Solution:

The given inequality is:

\[x^2 < 4\]

which derives to the quadratic equation \(\displaystyle x^2-4=0\).

Quadratic Formula

For a quadratic equation of the form \(a x^2 + bx + c = 0\), the roots are computed using the following quadratic formula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In this case, we have that the equation we need to solve is \(\displaystyle x^2-4 = 0\), which implies that corresponding coefficients are:

\[a = 1\] \[b = 0\] \[c = -4\]

First, we will compute the discriminant to assess the nature of the roots. The discriminating is computed as:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-4\right) = 16\]

Since in this case we get the discriminant is \(\Delta = \displaystyle 16 > 0\), which is positive, we know that the equation has two different real roots.

Now, plugging these values into the formula for the roots we get:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-4\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{16}}{2}\]

so then, we find that:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{16}=\frac{0}{2}-2\cdot 1=\frac{0}{2}-2=-2 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{16}=\frac{0}{2}+2\cdot 1=\frac{0}{2}+2=2\]

In this case, the quadratic equation \( \displaystyle x^2-4 = 0 \), has two real roots, so then:

\[\displaystyle x^2-4 = \left(x+2\right)\left(x-2\right)\]

so then the original polynomial is factored as \(\displaystyle p(x) = x^2-4 = \left(x+2\right)\left(x-2\right) \), which completes the factorization.

Analyzing Critical Points

The list of critical points found organized in ascending order is: \(-2\), \(2\).

Based on this, we need to analyze the following intervals:

• For the interval \(\left(-\infty, -2\right)\): The left-hand side is positive, so then \(\left(-\infty, -2\right)\) is not a part of the solution.

• For the interval \(\left(-2, 2\right)\): The left-hand side is negative, so then \(\left(-2, 2\right)\) is part of the solution.

• For the interval \(\left(2, \infty\right)\): The left-hand side is positive, which means that \(\left(2, \infty\right)\) is not a part of the solution.

Solution to the Inequality

Based on the inequality provided, and analyzing the critical points, we find that the solution to the inequality is: \(-2< x \le 2\).

Using interval notation, the solution is written as:

\[\left[-2,2\right)\]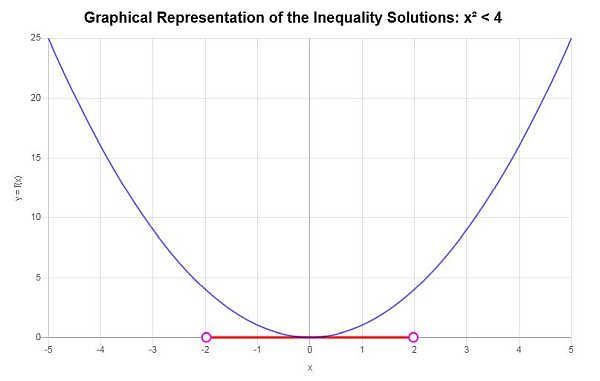

Other useful inequality calculators

The simplest inequality type you will be able to solve is linear inequalities. After that, you have quadratic inequalities, in terms of ease.

Then, you have polynomial inequalities in general, with degree higher than 2. Those should be straightforward, but they still could be formidable tasks in terms of the amount of laborious work required to solve them.

Having an inequality calculator for inequalities in general can really come in handy, as it will address the different types of inequalities that are amenable to the search of exact solutions.