More About the Normal Probability Plot

A normal probability plot is a plot that is typically used to assess the normality of the distribution to which the passed sample data belongs to.

There are different types of normality plots (P-P, Q-Q and other varieties), but they all operate based on the same idea. The theoretical quantiles of a standard normal distribution are graphed against the observed quantiles.

Therefore, if the sample data comes from a normality distributed population , then the normal probability plot should look like a 45 ^o line, with random variations about it. If that is not the case, and the pattern of the normal probability plot departs significantly/systematically from the normal probability plot, then one should suspect that the distribution is not normal.

How do you compute a normal probability plot?

There are several concrete steps you need to take, in a specific order to construct a normal probability plot

1. In this concrete case, the data are ordered in ascending order, and we call such data as \(X_1, X_2, ...., X_i , ...., X_n\).
2. For each \(X_i\) in this sequence of ordered data, we compute the theoretical frequencies \(f_i\), which are approximated using the following formula:
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. We then we also compute \(z_i\), is corresponding associated z-score as
\[ z_i = \Phi^{-1}(f_i)\]
4. Then, the normal probability plot is obtained by plotting the ordered X-values (your sample data) on the horizontal axis, and the corresponding \(z_i\) values on your vertical axis.

Normal probability plot Excel

You can plot a normal probability graph in Excel, but it takes some time. Yo

Calculators for the normal distribution and others

Other chart makers you can use are our normal distribution grapher , scatter plot maker or our Pareto chart maker .

Example: Calculation of a normal probability plot

Question: You are provided with the following sample data: 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 and 23. Construct a normal probability plot.

Solution:

We need to construct a normal probability plot. These are the sample data that have been provided:

Observation:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

The theoretical frequencies \(f_i\) need to be computed as well as the associated z-scores \(z_i\), for \(i = 1, 2, ..., 33\):

Observe that the theoretical frequencies \(f_i\) are approximated using the following formula:

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

where \(i\) corresponds to the position in the ordered dataset, and \(z_i\) is corresponding associated z-score. This iscomputed as

\[ z_i = \Phi^{-1}(f_i)\]

The following table is obtained

Position (i)	X (Asc. Order)	fi	zi
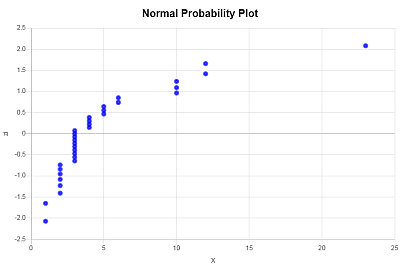
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

The normal probability plot is obtained by plotting the X-values (your sample data) on the horizontal axis, and the corresponding \(z_i\) values on your vertical axis. The following normality plot is obtained: