How to Solve for x

This calculator will allow you to solve for x for any given equation you provide, showing all the steps of the process in case that a solution can be found, which is not always the case .

You can provide an expression like 'y = x + 1' which is a simple linear function where x appears, or you can have something more complex , like 'x^2 + y^2 = 1', where you will have more than one solution.

Once you have provided a valid expression that involves x, you can click on "Calculate" for the process to get started, and the calculator will attempt to solve for x, by solving the equation needed. Notice the word "attempt", because you will find that some equations cannot be solved.

How do you solve for x?

There is not really one answer to that, as it heavily depends on the structure of the equation that x appears in. Linear equations will be simple to deal with as it is just about moving terms around and dividing the equality by a number if need.

Or for quadratic equations you will have a simple type of formula, the well know quadratic formula that will tell you exactly how to solve for x.

But for anything more complex than, it is no man's land, and each equation will require its own approach, if any, to be solved.

That is why having an equation calculator is so important, because it will have a way to solve the most common types of equation, plus it will have some tricks to try in case of a difficult one, increasing your chances of success.

Steps for solving for x

• Step 1: First, try to identify the type of equation: linear, quadratic, polynomial, rational, radical, logarithmic, exponential, etc.
• Step 2: If you have identified the type, then that specific type will have some specific rules to be solved. Ex: if you find that the equation for x is exponential, the usual trick for that kind of equations is to set a common base and equate exponents in order to solve the equation
• Step 3: If no specific type of equation has been identified, then you just can follow some generic type of roadmap: Try to isolate all the terms involving x on one side of the equation (Depending on the type of equation, that may not be possible)
• Step 4: Can you apply a suitable substitution? Can you simplify things by applying a function or some operation to both sides of the equality? That is pretty much the general advice to get you started

Honest, that is all about that you can know as a general rule to solve equations and to solve for x. The rest will come from the specific structure of the equation you are dealing with.

So, there is no formula for x?

Not in general, unfortunately. For the easier types, you will be able to find a formula for x, something like x = g(y), and sometimes this formula will help you define an inverse function, but sometimes you won't find any kind of formula, or sometimes you will find more than one solution.

Sometimes you will have to restrict the variables by solving an inequality in order to find a solution for x. This is, in such cases solving for x is successful only on some restricted region.

Is there a difference between solving for x and solving for y?

Yes, from the point of view that the target variable you want to solve would be different, but no from from a methodological point of view, as the steps you take to solve for x are the same steps you would take to solve for y.

Solving for x or y or z involves the same process, which is solving for a specific variable, which requires the same methodology. There are cases where symmetry plays a role, and it is even literally the same. Just to see it concretely, if you have the equation \(x^2+y^2=1\), solving for x would lead to the same exact steps than solving for y would. That is true only for this kind of symmetric equations.

Example: Solve for x

Find x in terms of y for : \(\frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\)

Solution: In this case we have a simple linear equation, so then solving for x is all about putting x on one side:

\[\frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\] \[ \Rightarrow \frac{1}{3} y = \frac{x-1}{x+4} - \frac{5}{6}\] \[ \Rightarrow \frac{1}{3} y + \frac{5}{6} = \frac{x-1}{x+4}\] \[ \Rightarrow \left( \frac{1}{3} y + \frac{5}{6} \right) (x+4) = x - 1\] \[ \Rightarrow x \left( \frac{1}{3} y + \frac{5}{6} \right) +4 \left( \frac{1}{3} y + \frac{5}{6} \right) = x - 1\] \[ \Rightarrow x \left( \frac{1}{3} y + \frac{5}{6} - 1\right) = - 1 - 4 \left( \frac{1}{3} y + \frac{5}{6} \right)\]

Then, by manipulating terms in the above equation, we obtain the solution:

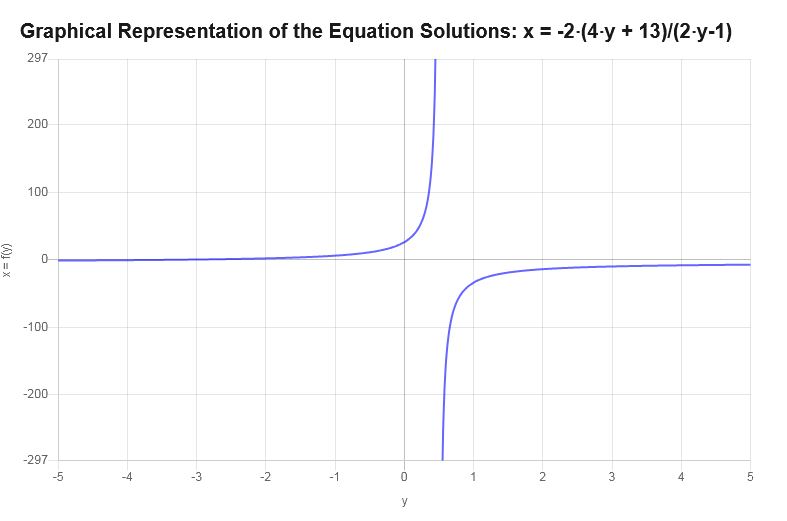
\[x=-\frac{2\cdot \left(4y+13\right)}{2y-1} \]

Therefore, solving for \(x\) for the given equation leads to the solution \(x=-\frac{2\cdot \left(4y+13\right)}{2y-1}\).

Graphically

The following is the graphical representation of the solutions obtained with \(y\) expressed in terms of \(\):

Example: Can you solve for x?

Can you solve for x in this case: \(y = x^2 - 1\)

Solution: In this case, we get directly that

\[y = x^2 - 1 \Rightarrow x^2 = y + 1\] \[ \Rightarrow x = \pm \sqrt{ y + 1 }\]

This implies that we are able to find two solutions, or "branches", which are \(x = \sqrt{ y + 1 }\) and \(x = -\sqrt{ y + 1 }\).

Other useful equation calculators

As we saw here, solving for x relies heavily in solving equations, which can certainly be a challenging process for the more complex types that are not linear or quadratic equations.

The idea of solving for x is tightly related with finding the inverse and also finding the graph of the inverse, as that is precisely how you start when you are dealing with inverses.

Equations can get more complicated when dealing with simultaneous equations, which require some specific techniques. One common procedure that we can deal with is solving systems of linear equations, using either graphical or analytical methods