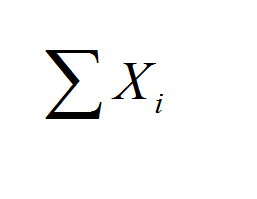Solvers Algebra

PEMDAS Calculator

Instructions: Use this calculator to compute and simplify any expression (numeric or symbolic) you provide, following the PEMDAS rules, showing all the steps. Please type in the expression you want to compute in the form box below.

About this PEMDAS calculator

This PEMDAS calculator will allow you simplify parentheses, multiplying expressions, divide expressions and add and subtract expressions, forming a compound more complex expression that can be solved with PEMDAS rules .

All you need to do is to provide a valid expression, either symbolic or numeric, and all the steps of the simplification will be shown to you.

Once a valid expression has been provided, the easy part comes in: you just need to click on the "Calculate" button, and that is it, all the steps will be there for you.

The process of simplifying expressions could be a nuanced one, especially if you provide the calculator with a complex expression.

What is PEMDAS meaning?

PEMDAS is an acronym that stands for:

P = Parentheses

E = Exponents

M = Multiplication

D = Division

A = Addition

S = Subtraction

The PEMDAS rule indicates the order of priority in which calculations should be done. This is, first parentheses, THEN exponents, THEN multiplications, and so on. So you can see this as an order of operations rule.

PEMDAS calculator with exponents

Does this calculator conduct PEMDAS for exponents? Absolutely! Indeed, PEMDAS has the 'E' for exponents, so then the exponents priority is very high in a simplification process, only surpassed by parentheses.

To a certain degree, parentheses and exponents allow you to see some 'isolated' expressions that can be handled separately. For example, if you had \(2^{\frac{1}{2} + \frac{1}{3}}\), the sum of fraction in the exponent is like 'isolated' and you can start simplifying there.

What are the steps for using PEMDAS?

Step 1: Start with the parentheses and exponents (in that order) seeing for sub-expressions that can be handled first
Step 2: Once those sub-expressions can be identified, use PEMDAS to solve them. This is, there may still be parentheses or exponents that need to be handled first and have priority
Step 3: When you have reached a foremost inner parentheses or exponent, you can see what simple operations remain, giving priority to multiplication and division, and then conducting additions and subtractions

Ultimately PEMDAS may be trivially applied in some trivial cases, but it is not always the case. PEMDAS has this potentially recursive nature, that could make its application confusing, especially with particularly complex, nested expressions.

In the end, in most of the cases you won't have to think too hard, as most of the usual cases are very simple, but it is good to have the awareness that PEMDAS can be as complex as the complexity of the provided expression you want to simplify .

Why is PEMDAS important?

PEMDAS is important because it is the only way we have to ensure that there is one and only way correct simplification. Now, there could be different paths leading to that correct simplification, but they will all be the same.

Simplifying expressions needs to be an exact endeavor, and that is what PEMDAS is all about, and a calculator that helps you with that can be certainly be useful.

Example: PEMDAS example

Calculate : \(\frac{1}{3} \frac{2}{3} + \frac{5}{4} - \frac{1}{6}\)

Solution: This is problem we can address with this order of operations calculator. Indeed, we are provided with the following expression: \(\displaystyle \frac{1}{3}\cdot\frac{2}{3}+\frac{5}{4}-\frac{1}{6}\).

The following calculation is obtained:

\( \displaystyle \frac{1}{3}\cdot \frac{2}{3}+\frac{5}{4}-\frac{1}{6}\)

We can multiply the terms in the top and bottom, and we get \(\displaystyle\frac{ 1}{ 3} \times \frac{ 2}{ 3}= \frac{ 2}{ 3 \times 3} \)

\( = \,\,\)

\(\displaystyle \frac{2}{3\cdot 3}+\frac{5}{4}-\frac{1}{6}\)

By multiplying the terms in the denominator, we get: \( 3 \times 3 = 9\)

\( = \,\,\)

\(\displaystyle \frac{2}{9}+\frac{5}{4}-\frac{1}{6}\)

Amplifying in order to get the common denominator 36

\( = \,\,\)

\(\displaystyle \frac{2}{9}\cdot\frac{4}{4}+\frac{5}{4}\cdot\frac{9}{9}-\frac{1}{6}\cdot\frac{6}{6}\)

We use the common denominator: 36

\( = \,\,\)

\(\displaystyle \frac{2\cdot 4+5\cdot 9-1\cdot 6}{36}\)

Expanding each term: \(2 \times 4+5 \times 9-6 = 8+45-6\)

\( = \,\,\)

\(\displaystyle \frac{8+45-6}{36}\)

Adding up each term in the numerator

\( = \,\,\)

\(\displaystyle \frac{47}{36}\)

which concludes the process of simplification.

Example: More PEMDAS examples. Order of operations problems

Simplify the following: \( \left(\frac{2}{3} + \frac{5}{4}\right)^2 - \frac{5}{6}\)

Solution: We are provided with the following expression: \(\displaystyle \left(\frac{2}{3}+\frac{5}{4}\right)^2-\frac{5}{6}\).

The following calculation is obtained:

\( \displaystyle \left(\frac{2}{3}+\frac{5}{4}\right)^2-\frac{5}{6}\)

Amplifying in order to get the common denominator 12

\( = \,\,\)

\(\displaystyle \left(\frac{2}{3}\cdot \frac{4}{4}+\frac{5}{4}\cdot \frac{3}{3}\right)\left(\frac{2}{3}\cdot \frac{4}{4}+\frac{5}{4}\cdot \frac{3}{3}\right)-\frac{5}{6}\)

We use the common denominator: 12

\( = \,\,\)

\(\displaystyle \left(\frac{2\cdot 4+5\cdot 3}{12}\right) \times \left(\frac{2\cdot 4+5\cdot 3}{12}\right)-\frac{5}{6}\)

Expanding each term: \(2 \times 4+5 \times 3 = 8+15\)

\( = \,\,\)

\(\displaystyle \left(\frac{8+15}{12}\right) \times \left(\frac{8+15}{12}\right)-\frac{5}{6}\)

Operating the terms in the numerator

\( = \,\,\)

\(\displaystyle \frac{23}{12}\cdot\frac{23}{12}-\frac{5}{6}\)

We can multiply the terms in the top and bottom as in \(\displaystyle\frac{ 23}{ 12} \times \frac{ 23}{ 12}= \frac{ 23 \times 23}{ 12 \times 12} \)

\( = \,\,\)

\(\displaystyle \frac{23\cdot 23}{12\cdot 12}-\frac{5}{6}\)

Multiplication of terms in the numerator and denominator, we get: \( 23 \times 23 = 529 \) and \( 12 \times 12 = 144\)

\( = \,\,\)

\(\displaystyle \frac{529}{144}-\frac{5}{6}\)

Amplifying in order to get the common denominator 144

\( = \,\,\)

\(\displaystyle \frac{529}{144}-\frac{5}{6}\cdot\frac{24}{24}\)

We use the common denominator: 144

\( = \,\,\)

\(\displaystyle \frac{529-5\cdot 24}{144}\)

Expanding each term in the numerator: \(529-5 \times 24 = 529-120\)

\( = \,\,\)

\(\displaystyle \frac{529-120}{144}\)

Operating the terms in the numerator

\( = \,\,\)

\(\displaystyle \frac{409}{144}\)

which concludes the process of simplification.

More algebra calculators

One of the cornerstones of algebra is the manipulation of algebraic expressions, from numbers, to fractions, to be complicated compound expressions.

All the guesswork is removed when having a proper set of rules establishing the correct order of operations in which expression should be simplified.

Along the same line of core Algebra rules simplifiers, you can also try our FOIL calculator, which uses PEMDAS to apply the distributive property in expression of the form \((a+b)(c+d\)