One-to-One Functions

This calculator will allow you assess whether or not a function is one-to-one, showing all the steps. The first thing you need to do is to provide the function. This could something simple, linear or quadratic like 'y = x^2 - 1', or you could decide to go for a rational function like 'f(x) = (x-1)/(x+3)'.

Then, we you are satisfied with what you have provided and you have made sure the function is valid, you click on the "Calculate" button, so to get all the steps of the process shown to you.

The concept of one-to-one function is a very important one in Algebra and Calculus. There many simple ways to test for one-to-one, one of them is the horizontal line test, but due to its nature, it is easier to use to disprove that a function is one-to-one. To prove that a function is one-to-one, we need an equation solving, analytic process.

What is a one-to-one process

Simply put, a one-to-one or injective function is one that for two different \(x_1\) and \(x_2\), the values of their images through \(f(x)\) is different, which means mathematically

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

Some instructors like to write it slightly differently, but still in an equivalent way: The function is one-to-one if

\[\displaystyle f(x_1) = f(x_2) \Rightarrow x_1 = x_2 \]

This is saying in a rather sophisticated way that, if the graph of the function crosses the same value (a horizontal line), then that happens only when the point is the same. So, all you are saying that there are no two different points where a horizontal line crosses it. So, you are just reiterating the horizontal line test.

How to check whether or not a function is one-to-ne

• Step 1: Start with the original function f(x), and set the equation y = f(x)
• Step 2: Attempt to solve for x
• Step 3: If you find more than one solution, then the function is NOT one-to-one, and if it has one solution or no solution, then the function is one-to-one

Normally, you will do some basic inspection to make sure that that function is clearly not one-to-one, possibly because you can easily find a horizontal line to make the HLT fail.

Then, you will look for some basic visual properties: Is the function always increasing (then it is one-to-one), and the same goes to the case where the function is always decreasing.

How is one-to-one related with finding the inverse

Stated in simple terms, in order to find the inverse of a function, the function MUST be one-to-one, at least on a certain sub-domain. Often times we do restrict the domain so we make a function 1-to-1 in a restricted domain, that it would not be 1-to-1 otherwise.

For example, \(f(x) = x^2\) is not one-to-one overall. Why, because you can take two different points \(x_1 = -1\) and \(x_2 = 1\) and find that \(f(x_1) = (-1)^2 = 1\) and \(f(1) = 1^2 = 1\), which means that the property (the one-to-one characterization)

\[\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \]

is not satisfied. Now, if instead of considering the full real line \(\R\), we consider only the positive values, we can conclude that the function is one-to-one on the positive real values (Hint: On that subdomain, the function is increasing)

Is there a formula to assess if a function is one-to-one?

Unfortunately not. I mean, one could think of \(\displaystyle x_1 \ne x_2 \Rightarrow f(x_1) \ne f(x_2) \), as the one-to-one formula, but this is rather a logical condition than a formula.

Though, there is a very broad, generic procedure that is used to test whether a function is one-to-one or not, which is what you see explained above. There is no "one-to-one formula". If we needed to settle for one, it should be y = f(x).

And, the we just solve for x. Nothing more, nothing less. Ultimately, it will depend what is f(x) all about. A very complex, convoluted function may pose lots of difficulties to be solved, and perhaps you need a function calculator for it, and even with a function calculator you may fail.

You probably are thinking, why is that?? It is because, at the heart of it, we don't have techniques to solve ALL equations. We just do what we can with some specific type of equations, but we are far away from knowing an EXACT way of solving all equations.

Example: One-to-One function

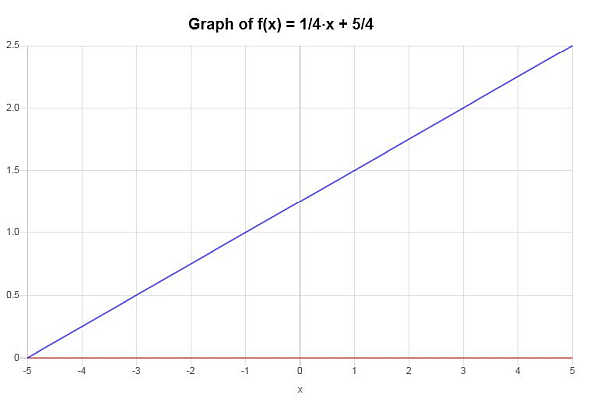
Is the following function injective: \(f(x) = \frac{1}{4} x + \frac{5}{4}\)

Solution:

We have been provided with the following function:

\[f(x) = \frac{1}{4} x + \frac{5}{4}\]

Then, in order to assess whether or not the given function is one-to-one, we need to solve for \(x\) and determine whether there is no solution, one solution, or multiple solutions. The starting equation is

\[y=\frac{1}{4}x+\frac{5}{4}\]

Putting \(x\) on the left hand side and \(y\) and the constant on the right hand side we get

\[\displaystyle -\frac{1}{4}x = -y -\left(-\frac{5}{4}\right)\]

Now, solving for \(x\), by dividing both sides of the equation by \(-\frac{1}{4}\), the following is obtained

\[\displaystyle x=-\frac{1}{-\frac{1}{4}}y+\frac{\frac{5}{4}}{-\frac{1}{4}}\]

and simplifying we finally get the following

\[\displaystyle x=4y-5\]

Therefore, the solving for \(x\) for given linear equation leads to \(x=4y-5\) and it is only one real solution, so then the given function is one-to-one.

Conclusion

Based on what has been found in the previous section, it can be concluded that the given function is one-to-one.

Graphically:

Example: 1-to-1 Function

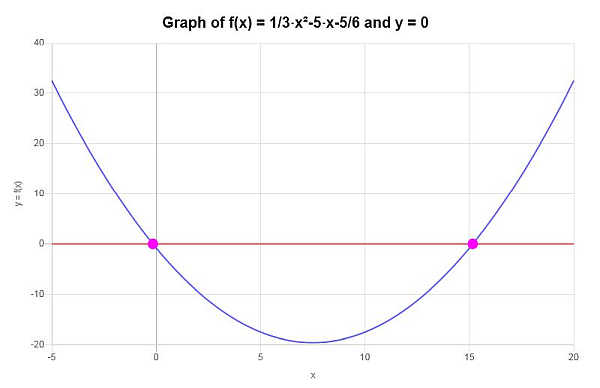
Prove or disprove that the following function is one-to-one: \(f(x) = \frac{1}{3} x^2 - 5x - \frac{5}{6}\)

Solution: In order to assess whether or not the given function is one-to-one, we need to solve for \(x\) and determine whether there is no solution, one solution, or multiple solutions. The starting equation we need to use is:

\[y=\frac{1}{3}x^2-5x-\frac{5}{6}\]

Initial Step: In this case, we first need to simplify the given equation, and in order to do so, we conduct the following simplification steps:

So then, the solutions are:

\[x_1=-\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \] \[x_2=\frac{1}{2}\sqrt{12y+235}+\frac{15}{2} \]

One-to-One Status

Based on the work shown above, it can be concluded that the given function IS NOT ONE-TO-ONE, since it does not pass the Horizontal Line Test, as for example the line \(y = 0\) is a horizontal line that crosses the given function more than once.

Graphically, the situation is be depicted as follows:

More interesting Algebra calculators

The concept of 1-to-1 functions is usually taken for granted, but it is a very important one, critical I would say. This is because the concept of one-to-one is tightly connected with the idea of monotone function (increasing or decreasing functions), all the same as it is tightly related to the calculation of the inverse function and its graph.

Yet, often times it is hard to the forest past the trees, as most crucial Algebra and Calculus concepts have tight links with each other. Function analysis is one of the things you will do all the time, so it is a good thing to acquire the skills to become good at that.