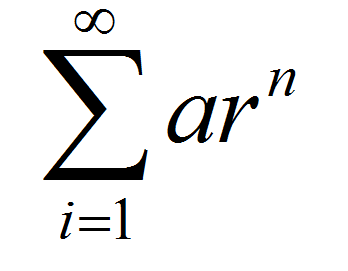Infinite Geometric Series Calculator
Instructions: Use this step-by-step Geometric Series Calculator, to compute the sum of an infinite geometric series by providing the initial term \(a\) and the constant ratio \(r\).
Observe that for the geometric series to converge, we need that \(|r| < 1\). Please provide the required information in the form below:
More about the infinite geometric series
The idea of an infinite series can be baffling at first. It does not have to be complicated when we understand what we mean by a series.
An infinite series is nothing but an infinite sum. In other words, we have an infinite set of numbers, say \(a_1, a_2, ..., a_n, ....\), and will add these terms up, like:
\[a_1 + a_2 + ... + a_n + ....\]But since it can be tedious to have to write the expression above to make it clear that we are summing an infinite number of terms, we use notation, as always in Math. An infinite series is written as:
\[ a_1 + a_2 + ... + a_n + .... = \displaystyle \sum_{n=1}^{\infty} a_n \]which is a more compact, unequivocal way of expressing what we mean. But yet, infinite sum idea is kind of confusing. What do we mean by infinite sum?
That is a good question: the idea of summing an infinite number of terms consists of adding up to a certain term \(N\) and then pushing this value \(N\) all the way to infinity. So precisely, an infinite series is defined as
\[ a_1 + a_2 + ... + a_n + .... = \displaystyle \sum_{n=1}^{\infty} a_n = \lim_{N\to \infty} \sum_{n=1}^{N} a_n \]So indeed, the above is the formal definition of the sum of an infinite series.
What is Special about a Geometric Series
In general, in order to specify an infinite series, you need to specify an infinite number of terms. In the case of the geometric series, you just need to specify the first term \(a\) and the constant ratio \(r\).
The general n-th term of the geometric sequence is \(a_n = a r^{n-1}\), so then the geometric series becomes
\[ \displaystyle \sum_{n=1}^{\infty} a_n = \displaystyle \sum_{n=1}^{\infty} a r^{n-1} \]An important result is that the above series converges if and only if \(|r| < 1\). In that case, the geometric series formula for the sum is
\[ S = \displaystyle \sum_{n=1}^{\infty} a r^{n-1} = \frac{a}{1-r}\]Examples
As an example, we can compute the sum of the geometric series \(1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, ....\). In this case, the first term is \(a = 1\), and the constant ratio is \(r = \frac{1}{2}\). So then, the sum is computed directly as:
\[ S = \displaystyle \sum_{n=1}^{\infty} a r^{n-1} = \frac{a}{1-r} = \frac{1}{1-1/2} = \frac{1}{1/2} = 2\]What happens with the series is \(|r| > 1\)
Short answer: the series diverges. The terms becomes too large, as with the geometric growth, if \(|r| > 1\) the terms in the sequence will become extremely large and will converge to infinity.
What if the sum is not infinite
In that case, you need to use this geometric sequence sum calculator , in which you add up a finite number of terms.