Solvers Calculus

Inverse Trig Derivatives

Instructions: Use this calculator to find derivatives of inverse trig functions, showing all the steps. Please type the function that contains an inverse trig function in the form box below.

Inverse Trig Derivatives

With this calculator you will be able to compute derivatives of inverse trig functions, showing all the steps of the process. The idea is that the function you provide contains an inverse trig function, for example f(x) = x^2/arctan(x+1), just to give an example. When you are ready and are done typing the function you need to differentiate, click on the "Calculate" button in order to see all the steps of the process and calculations. The idea of calculating derivatives of inverse trig functions is a natural one, and we will see in the next paragraphs that they can be directly derived from the trig derivatives that you know.

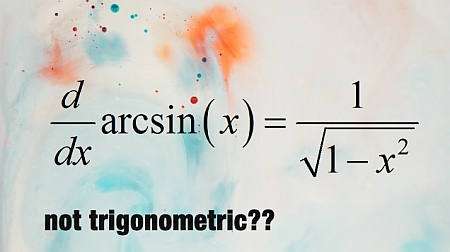
Inverse Trig Functions

In simple terms, the inverse trig function are those function that when evaluating them at the corresponding trig function, they lead to the identity. For example, if we consider the function

\sin(x)

, its inverse function is

\arcsin(x)

, and this inverse has the property that

\sin(\arcsin(x)) = x

as well as

\arcsin(\sin(x)) = x

for all $x$ on a certain interval. So strictly, $\arcsin(x)$ is the inverse function of $\sin(x)$ from an algebraic point of view. And the same goes for the other inverse trig functions and their corresponding trig functions.

Inverse Trig Derivatives calculation

So then, if $f$ is a function, and it has an inverse $f^{-1}$ , then we have that

f^{-1}(f(x)) = x

for all $x$ . Then, if we differentiate both sides of the equality, and we use the Chain Rule on the left side, we get

\displaystyle (f^{-1})'(f(x))f'(x) = 1

\displaystyle (f^{-1})'(f(x)) = \frac{1}{f'(x)}

Now, if we set $y = f(x)$ , then $x = f^{-1}(y)$ , which leads to

\displaystyle (f^{-1})'(y) = \frac{1}{f'(f^{-1}(y))}

\Rightarrow \displaystyle (f^{-1})'(x) = \frac{1}{f'(f^{-1}(x))}

How do we use this for inverse trig functions? Assume $f(x) = \sin(x)$ and $f^{-1}(x) = \arcsin(x)$ . Then, according to the general relationship between the derivative of a function and the derivative of its inverse, we get

\displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\frac{d}{dx}\sin (\arcsin(x))}

\Rightarrow \displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{\cos(\arcsin(x))}

But a neat geometric trick tells us that

\cos(\arcsin(x)) = \sqrt{1 - \sin^2(\arcsin(x))} = \sqrt{1 - x^2}

which implies that

\displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}

The rest of inverse trig derivatives are obtained with similar argument.

What are the 6 basic inverse trig functions?

#1: $\displaystyle \frac{d}{dx} \arcsin(x) = \frac{1}{ \sqrt{1 - x^2}}$
#2: $\displaystyle \frac{d}{dx} \arccos(x) = -\frac{1}{ \sqrt{1 - x^2}}$
#3: $\displaystyle \frac{d}{dx} \arctan(x) = \frac{1}{1+x^2}$
#4: $\displaystyle \frac{d}{dx} \operatorname{arccot}(x) = -\frac{1}{1+x^2}$
#5: $\displaystyle \frac{d}{dx} \operatorname{arcsec}(x) = \frac{1}{x \sqrt{x^2-1}}$
#6: $\displaystyle \frac{d}{dx} \operatorname{arccsc}(x) = -\frac{1}{x \sqrt{x^2-1}}$

Interestingly enough, when computing the derivative of inverse trig functions, none of the inverse trig derivatives involve either trig functions or inverse trig functions.

Applications of derivative of inverse trigonometric functions

Trig functions and their derivatives, as well as inverse trig functions and their derivatives form part of the inventory of basic functions and operations, used as building blocks, for creating more complicated functions.

Although trig functions will appear more often in applications than inverse trig functions, the latter also have a clear place in Calculus, especially when differentiating and using the partial fractions decomposition method.

Tips and tricks

Don't forget that the derivatives of inverse trig functions can be extremely useful, especially when integrating terms that have a quadratic denominator.

Also, it is easy to make mistakes when computing inverse trig derivatives by definition, you could definitely benefit from using a derivative calculator that will show the steps, or that you can use to check your work.

Example: Inverse Trig Derivatives

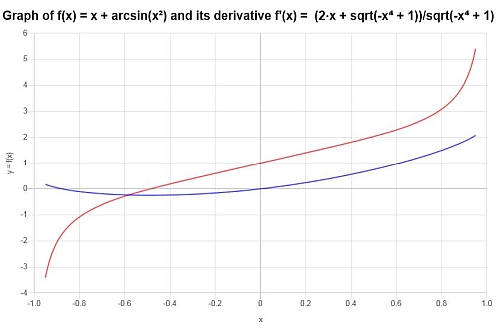
Calculate the derivative of: $f(x) = x + \arcsin(x^2)$

Solution: For this first example, we will analyze $\displaystyle f(x)=x+\arcsin\left(x^2\right)$ . This function involves an inverse trig function, compounded with another function. Let's compute its derivative:

\displaystyle \frac{d}{dx}\left(x+\arcsin\left(x^2\right)\right)

By linearity, we know

\frac{d}{dx}\left( x+\arcsin(x^2) \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin(x^2)\right)

, so plugging that in:

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)

But we know already that

\frac{d}{dx}\left(x\right) = 1

\displaystyle = \,\,

\displaystyle 1+\frac{d}{dx}\left(\arcsin\left(x^2\right)\right)

By using the Chain Rule:

\frac{d}{dx}\left( \arcsin\left(x^2\right) \right) = \frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}

\displaystyle = \,\,

\displaystyle 1+\frac{\frac{d}{dx}\left(x^2\right)}{\sqrt{1-\left(x^2\right)^2}}

In this case we use the Power Rule for polynomial terms:

\frac{d}{dx}\left( x^2 \right) = 2x

\displaystyle = \,\,

\displaystyle 1+\frac{2x}{\sqrt{1-\left(x^2\right)^2}}

which then leads to

\displaystyle = \,\,

\displaystyle 1+\frac{2x}{\sqrt{1-x^4}}

Answer: We can conclude that derivative of the function is:

f'(x) = \frac{2x+\sqrt{1-x^4}}{\sqrt{1-x^4}}

We can see both the function and its derivative in the following graph:

Example: More inverse trig derivatives

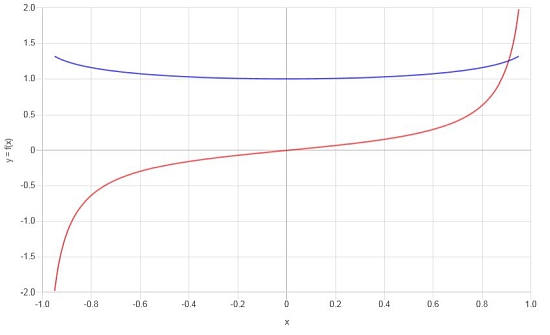
Consider the following function: $f(x) = \frac{\arcsin(x)}{x}$ , compute its derivative.

Solution: Now for the second example, we have the function $\displaystyle f(x)=\frac{\arcsin\left(x\right)}{x}$ .

\displaystyle \frac{d}{dx}\left(\frac{\arcsin\left(x\right)}{x}\right)

The Quotient Rule applies in this case:

\frac{d}{dx}\left( \frac{\arcsin\left(x\right)}{x} \right) = \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}

\displaystyle = \,\,

\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)\cdot \frac{d}{dx}\left(x\right)}{x^2}

We already know that

\frac{d}{dx}\left(x\right) = 1

\displaystyle = \,\,

\displaystyle \frac{x \cdot \frac{d}{dx}\left(\arcsin\left(x\right)\right)-\arcsin\left(x\right)}{x^2}

Directly differentiating:

\frac{d}{dx}\left( \arcsin\left(x\right) \right) = \frac{1}{\sqrt{1-\left(x\right)^2}}

\displaystyle = \,\,

\displaystyle \frac{x \cdot \frac{1}{\sqrt{1-\left(x\right)^2}}-\arcsin\left(x\right)}{x^2}

and then we get

\displaystyle = \,\,

\displaystyle \frac{\frac{1}{\sqrt{1-x^2}}x-\arcsin\left(x\right)}{x^2}

Finally, the following is obtained

\displaystyle = \,\,

\displaystyle \frac{-\left(\sqrt{1-x^2}\cdot \arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}

Final conclusion: The derivative we are looking for is:

f'(x) = \frac{-\left(\sqrt{1-x^2}\cdot\arcsin\left(x\right)-x\right)}{\sqrt{1-x^2}\cdot x^2}

Graphically, we have the following:

Inverse Trig Derivatives Example

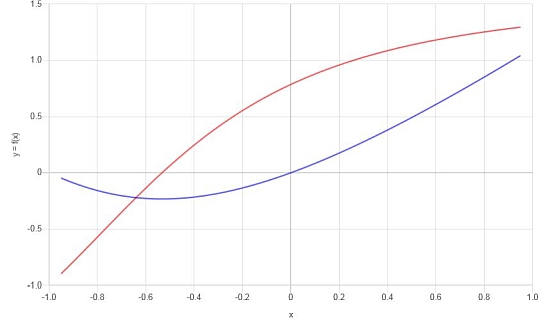
Calculate the derivative of: $f(x) = x \arctan(x+1)$

Solution: Now for this final example, we will work with the function $\displaystyle f(x)=x\arctan\left(x+1\right)$ , which contains an inverse function.

\displaystyle \frac{d}{dx}\left(x\arctan\left(x+1\right)\right)

The Product Rule applies in this case:

\frac{d}{dx}\left( x\arctan\left(x+1\right) \right) = \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{d}{dx}\left(\arctan\left(x+1\right)\right)

Using the Chain Rule:

\frac{d}{dx}\left( \arctan\left(x+1\right) \right) = \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x+1\right)}{1+\left(x+1\right)^2}

By linearity, we know

\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)

, so plugging that in:

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)}{1+\left(x+1\right)^2}

The derivative of a constant is 0, so then:

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{\frac{d}{dx}\left(x\right)}{1+\left(x+1\right)^2}

We know that

\frac{d}{dx}\left(x\right) = 1

\displaystyle = \,\,

\displaystyle \frac{d}{dx}\left(x\right) \cdot \arctan\left(x+1\right)+x \cdot \frac{1}{1+\left(x+1\right)^2}

and then we get

\displaystyle = \,\,

\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)^2}+\arctan\left(x+1\right)

We expand the terms:

\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)

\displaystyle = \,\,

\displaystyle \frac{x\cdot 1}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)

Reducing the one in

x\cdot 1 = x

\displaystyle = \,\,

\displaystyle \frac{x}{1+\left(x+1\right)\left(x+1\right)}+\arctan\left(x+1\right)

Finally, the following is obtained

\displaystyle = \,\,

\displaystyle \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}

Conclusion: After simplifying, the derivative is:

f'(x) = \frac{x^2\arctan\left(x+1\right)+2x\arctan\left(x+1\right)+x+2\arctan\left(x+1\right)}{x^2+2x+2}

Based on the results found, we can construct the following graph for f and f':

Other Calculus calculators

When using trig derivatives, we stated that they were crucial building blocks for applying basic derivative rules .

Derivatives for inverse trig functions can be derived simply from the derivatives of basic trig derivatives, and that is why we also consider them within the group of basic derivatives to learn or even memorize.