Solvers Calculus

Implicit differentiation calculator

Instructions: Use this implicit differentiation calculator to compute derivative \(\frac{dy}{dx}\), when \(x\) and \(y\) are linked via an equation. Provide an equation that involves x and y in the form box below.

Implicit Differentiation

This calculator will help you to conduct implicit differentiation for an equation that involves the variables x and y. You need to provide a valid equation like x^2 + y^2 = 1, or xy - x^2 y^2 = 0, etc.

Once you provide a valid equation involving two variables (\(x\) and \(y\)), all you have to do is click on the "Calculate" button, and all the steps of the corresponding implicit differentiation will be shown.

This is a dy/dx calculator with steps in the sense that it will show you all the relevant steps of the calculation of the derivative of one variable with respect to another, as long as those two variables are related in one equation. This relationship is what allows you to find the corresponding implicit derivative.

Having an equation that related the two variables \(x\) and \(y\) tells us that we should be able to express \(y\) as a function of \(x\) and write \(y = y(x)\). Often, we cannot explicitly express \(y\) as a function of \(x\) we assume there is such function, in which case, it makes sense to differentiate \(y\) with respect to \(x\).

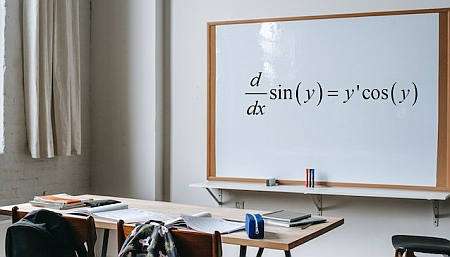
What is implicit differentiation?

Implicit differentiation is a differentiation calculation technique based on the assumption that it is possible to state from a given equation involving \(x\) and \(y\) that \(y\) is a function of \(x\) though often times we cannot write explicitly such function.

Once that assumption is made, we assume that we can compute \(\frac{dy}{dx}\) and we can use all the known derivative rules (product rule, quotient rule and chain rule) to differentiate both sides of the equation, and solve for \(\frac{dy}{dx}\).

What is the implicit differentiation method?

The implicit differentiation method is a method that allows you to compute a derivative to expressions that are not directly put in \(f(x)\) format. This is, when given a function of a variable \(x\) for example, we just simply go ahead and differentiate that function.

But when two variables \(x\) and \(y\) are related via an equation, like \(x^2+y^2 = 1\) for example, you may also differentiate y with respect to x, under the traditional method, you will need to SOLVE y in terms of x, and THEN you can differentiate.

Using implicit differentiation, you can differentiate directly, by only making the assumption that \(y = y(x\), and making use of the chain rule.

Steps for using implicit differentiation

Step 1: Identify the equation that involves two variables x and y. Simplify any redundant terms
Step 2: Assume that y is a function of x, y = y(x), so it makes sense to compute the derivative of y with respect to x
Step 3: Calculate the derivative of both sides of the equation using all the derivative rules you need. This will lead to an equality in which x, y and y' are present potentially
Step 4: Solve what you got in Step 3 for y'. Note that y' will usually be written as a function of x and y, which is fine, since y also depends on x

This is a very general methodology, and it will have subtleties from case to case, but that is the blueprint that should work in most cases, with the added potential algebraic manipulations difficulty.

Why using a implicit differentiation calculator

Implicit differentiation could be confusing at times, if you are not very clear on what you differentiating, and respect to what variable. A calculator will help you compare your result and one special thing about our calculator is that all the steps of the process are shown.

That is a crucial help for you, because it will show you exactly what derivative rule, and where you applied it.

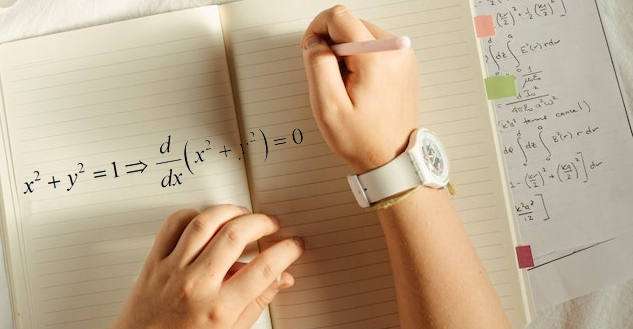
What is the point of implicit differentiation?

That is a fair question. If you have an equation involving x and y, why not solving y in terms of x and using regular derivative calculation to get the derivative of y with respect to x. I can give you at least two good reasons:

Reason 1: It may be the case that you CANNOT solve y in terms of x explicitly. There may be a function, but you cannot simply find it. Think of y + tan(y) = x^2
Reason 2: Even if you happen to solve y in term of x, it may be a really complicated expression, and the derivative calculation could be very convoluted and difficult. Usually, implicit differentiation is algebraically simple, in relative terms

Does the implicit derivative depend on y?

Not always, but often. Now, this only saying that \(\frac{dy}{dx}\) can depend on x and y, but since y depends on x, it is just saying that as expected \(\frac{dy}{dx}\) depends on x.

Different implicit differentiation examples will be presented in the following section.

Second implicit derivative

One question is: can compute the second derivative using implicit differentiation? The answer is YES. You just do the same as with the first derivative using implicit differentiation, you simply assume that \(y\) is a function of \(x\), so you write \(y = y(x)\), and you can differentiate as much as you wish.

For example, say you want to find \(\frac{d^2y}{dx^2}\) given the equation \(x^2+y^2=1\). Differentiating both sides with respect to \(x\):

\[ \frac{d}{dx}\left(x^2+y^2\right)=\frac{d}{dx}\left(1\right)\] \[ \Rightarrow 2x+2yy' = 0\]

Now, you differentiate again with respect to x:

\[ \frac{d}{dx}\left(2x+2yy'\right)=\frac{d}{dx}\left(0\right)\] \[ \Rightarrow 2+2(y')^2+2yy'' = 0\]

and now we solve for \(y''\):

\[ \Rightarrow y'' = -\frac{(2+2(y')^2)}{2y}\] \[ \Rightarrow y'' = -\frac{(1+(y')^2)}{y}\]

Example: Implicit Differentiation Example

Find \(\frac{dy}{dx}\) for the equation: \(x^2 - y^2 = 2y\)

Solution: This is an example of implicit differentiation. The following equation has been provided: \(\displaystyle x^2-y^2=2y\), for which we need to conduct a implicit differentiation, where we assume that \(y\) is a function of \(x\) .

The equation does not need further simplification, so we can proceed with the implicit differentiation:

We need to differentiate both sides of the equation with respect to \(x\), and on both sides we assume that \(y = y(x)\).

Left side: Differentiating the left side with respect to \(x\)

\( \displaystyle \frac{d}{dx}\left(x^2-y^2\right)\)

By linearity, we know \(\frac{d}{dx}\left( x^2-y^2 \right) = \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(x^2\right)-\frac{d}{dx}\left(y^2\right)\)

Using the Chain Rule: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) and using the Power Rule for polynomial terms: \(\frac{d}{dx}\left( x^2 \right) = 2x\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2x-2y\cdot \frac{dy}{dx}\)

Right side: Differentiating the right side with respect to \(x\)

\( \displaystyle \frac{d}{dx}\left(2y\right)\)

Since it is a constant times \(y\), we directly get: \(\frac{d}{dx}\left( 2y \right) = 2 \cdot \frac{d}{dx}\left(y\right)\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{d}{dx}\left(y\right)\)

We assume that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle 2 \cdot \frac{dy}{dx}\)

Therefore, the following is obtained after differentiating both sides with respect to \(x\):

\[\displaystyle 2x-2y\frac{dy}{dx} = 2\frac{dy}{dx}\]

Putting all the terms on one side:

\[-2\,y\frac{d}{dx}y+2\,x-2\,\frac{d}{dx}y = 0\]

Grouping everything that contains \(\displaystyle \frac{dy}{dx}\):

\[-2\,{\left(y+1\right)}\frac{d}{dx}y+2\,x = 0\]

Finally, solving for \(\displaystyle \frac{dy}{dx}\), leads to:

\[\displaystyle \frac{dy}{dx} = \frac{x}{y+1}\]

Example: More implicit differentiation Calculations

What is the slope of the tangent line to a unit circle at the point \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\)

Solution: Notice that the equation of the unit circle is \(\displaystyle x^2 + y^2 = 1\), which defines implicitly \(y\) as a function of \(x\). In order to find the tangent line, we need to compute \(\frac{dy}{dx}\) at the specified point. Using implicit differentiation, we differentiate both sides of the equation that defines the unit circle: \[\displaystyle x^2 + y^2 = 1\] \[\Rightarrow \displaystyle \frac{d}{dx}\left(x^2 + y^2\right) = \frac{d}{dx}\left(1\right)\] \[\Rightarrow \displaystyle 2x+2yy' = 0 \] \[\Rightarrow \displaystyle 2yy' = -2x \] \[\Rightarrow \displaystyle y' = -\frac{x}{y} \]

The point of interest is \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\), so then .

\[\displaystyle y' \left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) = -\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}} = -1\]

This implies that the slope of the tangent line at the point \(\left(\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right)\) is \(m = -1\), which implies that the equation of the tangent line at that point is

\[\displaystyle y - \frac{\sqrt{2}}{2} = -\left(x-\frac{\sqrt{2}}{2}\right)\] \[\Rightarrow \displaystyle y = \frac{\sqrt{2}}{2} - x + \frac{\sqrt{2}}{2}\] \[\Rightarrow \displaystyle y = \sqrt{2} - x \]

Example of implicit differentiation

Consider the equation: \( \displaystyle \frac{2}{3} x + y^2 = \frac{2}{5} \). Compute \(\frac{dy}{dx}\)

Solution: In this case we have the following equation: \(\displaystyle \frac{2}{3} x + y^2 = \frac{2}{5}\), so we need to do implicit differentiation, under the assumption that \(y\) depends on\(x\) .

Further simplification of the equation is not required, so then allowing us to proceed with the implicit differentiation:

Now we need to compute the derivative of both sides with respect to the variable \(x\), assuming that \(y = y(x)\).

Left side: Differentiating the left side with respect to the variable \(x\)

\( \displaystyle \frac{d}{dx}\left(\frac{2}{3}x+y^2\right)\)

Using linearity, we know \(\frac{d}{dx}\left( \frac{2}{3}x+y^2 \right) = \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\), so plugging that in:

\( \displaystyle = \,\,\)

\(\displaystyle \frac{d}{dx}\left(\frac{2}{3}x\right)+\frac{d}{dx}\left(y^2\right)\)

We have to use the Chain Rule: \(\frac{d}{dx}\left( y^2 \right) = 2y\cdot \frac{d}{dx}\left(y\right)\) and directly we get: \(\frac{d}{dx}\left( \frac{2}{3}x \right) = \frac{2}{3}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2}{3}+2y\cdot \frac{d}{dx}\left(y\right)\)

Assuming that \(y\) is a function of \(x\): \(\frac{d}{dx}\left( y \right) = \frac{dy}{dx}\)

\( \displaystyle = \,\,\)

\(\displaystyle \frac{2}{3}+2y\cdot \frac{dy}{dx}\)

Right side: Now we differentiate the right side with respect to \(x\)

\( \displaystyle \frac{d}{dx}\left(\frac{2}{5}\right)\)

The expression is a constant, so its derivative is 0

\( \displaystyle = \,\,\)

\(\displaystyle 0\)

Hence, the result that is obtained after differentiating both sides with respect to \(x\) is:

\[\displaystyle \frac{2}{3}+2y\frac{dy}{dx} = 0\]

Therefore, we can now solve for \(\displaystyle \frac{dy}{dx}\) to get:

\[\displaystyle \frac{dy}{dx} = -\frac{1}{3\,y}\]

More useful Calculus solvers

One of the most interesting applications of the rules of derivatives is the concept of implicit differentiation. It has applications in Physics, Economics and Engineering, and it is extremely practical to describe the rate of change along curves.

A different type of derivatives are partial derivatives in which, as opposed to the case of implicit differentiation where we assume that y = y(x), in that case y is considered a constant when x changes.