More About Sampling Distribution of the Sample Proportion

The sample proportion is defined as $\displaystyle \hat p = \frac{X}{n}$, where $X$ is the number of favorable cases and $n$ is the sample size. This situation can be conceived as $n$ successive Bernoulli trials $X_i$, such that $\Pr(X_i = 1) = p$ and $\Pr(X_i = 0) = 1-p$. In this context, the number of favorable cases is $\displaystyle \sum_{i=1}^n X_i$, and the sample proportion $\hat p$ is obtained by averaging $X_1, X_2, ...., X_n$. This indicates that when the sample size is large enough we can use the normal approximation by virtue of the Central Limit Theorem.

The mean and standard error of the sample proportion are:

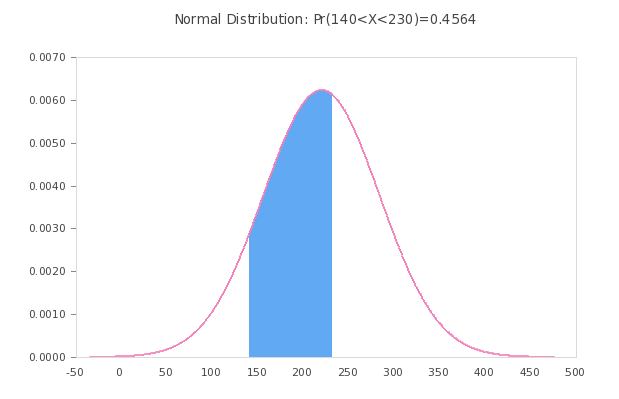
Therefore, when the sample size is large enough, and $np \geq 10$ and $n(1-p) \geq 10$, then we can approximate the probability $\Pr( p_1 \le \hat p \le p_2)$ by

It is customary to apply a continuity correction factor $cf = \frac{0.5}{n}$ to compensate for the fact that the underlying distribution is discrete, especially when the sample size is not sufficiently large. If you are looking for the sampling distribution of the sample mean, use this calculator instead