Differential Calculator
Instructions: Use this differential calculator, to find the differential of a function you provide, at a given point that you provide, showing all the steps. Please type the function and the point in the form box below.
Differential Calculator
This calculator will allow you to compute the differential of a function you provide, at a point you provide, showing all the steps of the process.
The function you provide can be any valid differentiable function like f(x) = x^2 + 2x, or f(x) = x^2*sin(x), just to mention two examples.
Then, when you have provided the function and the point for the differential calculation, just click on "Calculate" so to get all the steps of the process shown.
The idea of differential is tightly with that of tangent line and linear approximation, as the differential is precisely measuring the variation of y, along the tangent line at the given point.
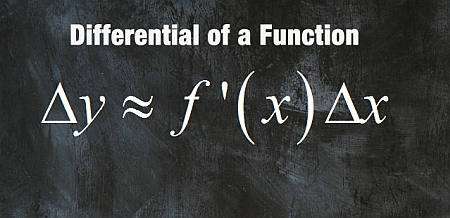
What is a differential?
In differential calculus, the idea is that derivatives give you information about the instant rate of change of a function at a given point.
The concept of differential uses the rate of change determined by the derivative at a given point \(x_0\) to approximate the behavior of the function by its tangent line.
The formula of the differential is based on the idea that
\[\displaystyle \Delta y \approx f'(x_0) \Delta x \]where \(\Delta y = y - f(x_0)\) and \(\Delta x = x - x_0\). For the differential \(dy\), we define
\[\displaystyle dy = f'(x_0) dx \]This (loose) definition is based on the idea that the linear approximation and the function approach to the same behavior when \(x\) is sufficiently close to \(x_0\).
Steps for computing a differential
- Step 1: Identify the function f(x) and the point x0 at which you want to compute the differential
- Step 2: Compute the derivative f'(x) and evaluate it at x0, so you get f'(x0). Simplify it, if needed
- Step 3: Use the formula \(\displaystyle dy = f'(x_0) dx \)
Sometimes you will find the differential written as \(\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \), as a form of indicating that you will use the differential to estimate changes in y, measured by \(\Delta y\).
Differential Calculator dy
Using a differential calculator can save you time with the process of calculation of the derivative. The idea of the differential has always been a strange one, in the sense that it appears to be loosely defined.
Though there is a way of define differentials and their operations formally (a subject called Differential Forms), most mathematicians don't see a reason for differentials to exist, as their don't provide any new information that the derivative or the first order approximation do not provide.
Total Differential Interpretation
The most common application and interpretation of the differential is when used in its 'finite' expression:
\[\displaystyle \Delta y = f'(x_0) \Delta x = f'(x_0)(x-x_0) \]where you are looking to estimate the variation in y, as measured by \(\Delta y\), from the variation in x, as measured by \(\Delta x\) and the derivative at the point.
Sometimes this \(\Delta y\) is called the total variation or total differential.
Tips and Tricks
Don't forget that the differential can be taken as a theoretical definition, \(\displaystyle dy = f'(x_0) dx \), which indicates the infinitesimal variation in y cause by an infinitesimal variation in x.
It also can be used in its total differential form, in which you have
\[\displaystyle \Delta y \approx f'(x_0)(x-x_0)\]which tells you an approximated variation in y, when for a change in x (from \(x_0\) to \(x\)).
The center of all algebraic calculator starts with the power of basic numbers of fractions.
Example: Differential Calculator
Consider the function: \(f(x) = x^2\). Find its differential at the point \(x_0 = 1\).
Solution: In the case of this first example, we work with the function \(\displaystyle f(x)=x^2\), for which we need to compute its differential at the point \(x_0 = 1\).
The function came already simplified, so we can proceed directly to compute its derivative:
Differential: The formula for the differential for the function \(\displaystyle f(x)=x^2\) at the point \(x_0 = 1\) is:
\[dy = f'(x_0)(x - x_0) \]We define \(\displaystyle y_0 = f(x_0)\), so then plugging the value of the point \(x_0 = 1\) in the function leads to:
\[y_0 = f(x_0) = f\left(1\right) = 1^2 = 1\]Also, plugging the value of the point \(x_0 = 1\) at the calculated derivative leads to:
\[f'(x_0) = f'\left(1\right) = 2\cdot 1 = 2 \]So then, we now plug in this value into the differential formula to get:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = 2\left(x-1\right) \]\[\Rightarrow dy = 2x-2 \]Conclusion: Therefore, we find that the differential for the function \(\displaystyle f(x)=x^2\) at the point \(x_0 = 1\) is:
\[dy = 2x-2 \]Example: Differential Calculation
For the given function: \(f(x) = x^3 + 3x^2 - 2\), find the differential at the point \(x_0 = 2\).
Solution:Now, the function we need to find the differential for is \(\displaystyle f(x)=x^3+3x^2-2\),
Differential Calculation: We use the following formula for the differential that we need to construct for the given function \(\displaystyle f(x)=x^3+3x^2-2\), at the given point \(x_0 = \frac{1}{2}\) is:
\[dy = f'(x_0)(x - x_0) \]Observe that \(\displaystyle y_0 = f(x_0)\), which means that evaluating the function at \(x_0 = \frac{1}{2}\) we find:
\[y_0 = f(x_0) = f\left(\frac{1}{2}\right) = \left(\frac{1}{2}\right)^3+3\left(\frac{1}{2}\right)^2-2 = -\frac{9}{8}\]Then, we get the derivative at the point \(x_0 = \frac{1}{2}\):
\[f'(x_0) = f'\left(\frac{1}{2}\right) = 3\left(\frac{1}{2}\right)^2+6\cdot \frac{1}{2} = \frac{15}{4} \]Hence, we get the following
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(\frac{15}{4}\right)\left(x-\frac{1}{2}\right) \]\[\Rightarrow dy = \frac{15}{4}x-\frac{15}{8} \]Conclusion: The final conclusion is that the differential we are looking for is given by:
\[dy = \frac{15}{4}x-\frac{15}{8} \]Differential Example
We are given the function: \(f(x) = \frac{\sin(x)}{x}\). Find its differential at the point \(x_0 = \frac{\pi}{2}\).
Solution:
The following function has been provided: \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), for which we need to compute its differential at the point \(x_0 = \frac{\pi}{2}\).
The function came already simplified, so we can proceed directly to compute its derivative:
Calculation: Now it is time to find the differential associated to \(\displaystyle f(x)=\frac{\sin\left(x\right)}{x}\), for the given point \(x_0 = \frac{\pi}{2}\). The formula used is:
\[dy = f'(x_0)(x - x_0) \]We plug the value of the point \(x_0 = \frac{\pi}{2}\) in the calculated derivative, which leads to:
\[f'(x_0) = f'\left(\frac{\pi}{2}\right) = \frac{\cos\left(\frac{\pi{}}{2}\right)}{\frac{\pi{}}{2}}-\frac{\sin\left(\frac{\pi{}}{2}\right)}{\left(\frac{\pi{}}{2}\right)^2} = -\frac{4}{\pi{}^2} \]Therefore, using the differential formula:
\[dy = f'(x_0)(x - x_0) \]\[\Rightarrow dy = \left(-\frac{4}{\pi{}^2}\right)\left(x-\frac{1}{2}\pi{}\right) \]\[\Rightarrow dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Conclusion: The corresponding differential is:
\[dy = \frac{2}{\pi{}}-\frac{4x}{\pi{}^2} \]Other differentiation calculators
Finding derivatives is without a question a key element in Calculus. Derivatives provide the information required to understand the rate of change of functions. as those have an intimate connection.
Fortunately, finding derivatives is a systematic process (not necessarily easy) if you follow specific differentiation rules. The most commonly used rules are the product rule, quotient rule and chain rule.
Linear or first order approximations conceptually attempt to approximate a function by a line, at least locally, and can tell you a lot about the behavior of a function, close to a certain point.