Inequality Calculator
Instructions: Use inequality calculator to solve any inequality that you provide, showing all the steps. Please type in the inequality you want to solve in the box below:
More about solving inequalities
With this calculator you will be able to solve inequalities that you provide. All you have to do is to type your desired inequality in the box, and also make sure that you are providing a valid inequality.
For example, you could provide something like '2x^2 - x >= 1/2', or something like 'sin(x) > 0', as long as you provide valid ones. Also make sure that you use an inequality sign, such as ">", "<", ">=" or "<=".
If instead you use "=", then this calculator will act as an equation calculator.
Once you provide a valid inequality, the next step is to click on "Solve", and in a fraction of a second you will be presented with the step-by-step solution. One caveat: not all inequalities will be able to be solved, so keep that in mind.
Not all inequalities are easy to solve, nor we can apply some preconceived methods. Only some types, such as linear inequalities, quadratic inequalities or polynomial equalities (for lower degrees) admit a systematic treatment.

What is an inequality?
An inequality is a type of math object that is very similar to a math equation, with the difference that instead of "=", an inequality contains either ">", "<", ">=" or "<=". This small difference in appearance still add more complexities to solving an inequality than an equation.
For example, the expression below is an inequality
\[\displaystyle x + \frac{1}{3} < x^2 \]So, it is an math expression that has two sides, the left-hand side and the right-hand side, and it has "<" as the corresponding inequality sign. The above inequality is said to be a quadratic inequality, because the expressions on the left and right hand sides are both polynomial, and the highest degree is 2.
Now, for example, the inequality below is a trigonometric inequality:
\[\displaystyle x + \frac{1}{3} \le \sin\left(x^2 + \frac{1}{x}\right) \]It is an inequality because it has the inequality sign \(\le\), and the right hand side contains a trigonometric expression. Observe that the first inequality is quite simple to solve, whereas the other hand is far from being easy, and you actually cannot solve it.
How to solve an inequality
In general terms, we will find the solution to inequalities by solving first an associated equation. Solving the inequality will be harder when the associated equation is harder to solve. The following steps will help you in the solution process:
- Step 0: Simplify the expressions involved in the inequality. It is almost always easier to solve a simplified inequality than it is to solve the original one
- Step 1: Identify the inequality you want to solve, and carefully identify the inequality sign (>, ≥, <, ≤). If you have "=", you should then use an equation calculator instead
- Step 2: You then write down the associated equation, which is simply obtained by replacing the inequality sign found in the previous step, and then replacing it by the equality sign "="
- Step 3: Solve the associated equation. You will determine the solution of the inequality based on the existence of real solutions to your associated equation, and taking notes on any points that may make the expression undefined
- Step 4: If your associated equation has no real solution: In that case, you know that the equation is never zero, at least for real values. Then, and assuming continuity, either all points are a solution of the inequality or none is. So you evaluate the inequality at any point (say x = 0), and if it holds, then all real values are solution to the inequality, and if it does not, then there are no real solutions
- Step 5: Finally, suppose that there are real solutions to the associated equation. We will call those critical points, and we will add any points where the expression becomes undefined (divisions by zero, etc) to the list of critical points
- Step 6: If there is only one critical point, which we call 'a' : Evaluate the inequality at any point to the left of 'a', and if it holds, the interval (-∞, a) will be part of the solution set. If the inequality is "<=" or ">=", then you include the end point Finally, (-∞, a). You take a similar step for a point to the right of 'a', and if inequality holds for it, then (-∞, a) will be part of the solution set
- Step 7: A similar process is carried if more than one critical point exist: Take two consecutive critical points, which we call 'a1' and 'a2': Evaluate the inequality at any point in between a1 and a2, and if it holds, the interval (a1, a2) will be part of the solution set. If the inequality is "<=" or ">=", then you include the end points
It seems complicated, but you just have to be systematic. For example, if your inequality is \(\displaystyle x + \frac{1}{3} < x^2 \), then then associated equation is \(\displaystyle x + \frac{1}{3} = x^2 \), which is easy to solve, since it is a quadratic equation.
Then, in the context of analyzing the critical points (if any), graphing the inequality solution may make things more clear. In some Algebra classes they teach students to use a tabulation to keep track of what happens in between critical points, which could be really useful.
What is the difference with a system of inequalities?
A system of inequalities consists of several simultaneous inequalities that need to be solved at the same time. It sounds harder than solving a simple inequality because it is harder. If solving inequalities can be laborious, even more so for system of inequalities.
An example of a system of inequalities is shown below:
\[\displaystyle x + y < 1 \] \[\displaystyle 2x + y^2 \le 1 \]In the example above you have of a system of inequalities to be solved. This system of inequalities has two inequalities and two unknowns (x and y).
As you can probably imagine, solving a system of inequalities can be difficult in general. Mostly, we will focus on solving system of linear equations, which are tightly related to solving a system of linear equations

Advantages of using this inequality calculator with steps
Really, solving most inequalities will be hard. Only a selected few of them with very specific structures will lend themselves to be analyzed. Majority will not, so you better be prepared for that.
- Advantage 1: Save lots of time: Solving inequalities can take a long time, as you first need to solve the associated equation and then analyze critical points
- Advantage 2: Make sure you give the best shot at solving it: As you probably know now, not all equations or inequalities can be easily solved, or solved at all. A calculator with steps will try the best possible approach based on the structure detected
- Advantage 3: Get results, step-by-step in a neat way. Some calculators will give you the final answer but won't show steps. A graph depicting the solutions will also come in handy
While you learn the ropes, having an inequalities calculator that does the heavy lifting for you will show you the way of how things are done, and likely you will acquire the skills needed to detect the structures that are easier to tackle.
Is there any practical use for inequalities?
You bet! In basic math (Algebra and Calculus 101), there is a stronger emphasis on equalities and equations. The real world is full of process where we don't necessarily have equations, but we do have inequalities that come from lower or upper bound imposed by some physical constraints.
Certain advanced math fields like Differential Equations base their theoretical frameworks on inequalities (which the experts like to call "energy estimates" in some contexts).
The importance of inequalities may not be apparent to you, nor the need to learning them too urgent, but truly, inequalities do form one of the cornerstone of the math methodology used to construct theories, though in the pretty final results we tend to see equalities instead.

Example: Solving inequalities
Calculate the solution to: \(\frac{1}{3}x + \frac{5}{4} \ge \frac{1}{6}\)
Solution: We need to put all terms of the inequality on the left-hand side (could be the right-hand side but it is rather conventional to use the left):
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6}\ge 0 \]From the above inequality, we obtain the associated linear equation that needs to be solved first:
\[\frac{1}{3}x + \frac{5}{4} - \frac{1}{6} = 0 \]Step 0: In this case, we first need to simplify the given linear equation, and in order to do so, we conduct the following simplification steps:
Solving the Linear Equation
Putting \(x\) on the left hand side and the constant on the right hand side we get
\[\displaystyle \frac{1}{3}x = -\frac{13}{12}\]Now, solving for \(x\), by dividing both sides of the equation by \(\frac{1}{3}\), the following is obtained
\[\displaystyle x = \displaystyle \frac{ -\frac{13}{12}}{ \frac{1}{3}}\]and simplifying we finally get the following
\[\displaystyle x=-\frac{13}{4}\]Therefore, the solving for \(x\) for given linear equation leads to \(x=-\frac{13}{4}\).
Critical Points Analysis
The only critical point that was found is \(-\frac{13}{4}\).
Based on this, we need to analyze the following intervals:
• For the interval \(\left(-\infty, -\frac{13}{4}\right)\): The left-hand side is negative, so then \(\left(-\infty, -\frac{13}{4}\right)\) is not part of the solution.
• For the interval \(\left(-\frac{13}{4}, \infty\right)\): The left-hand side is positive, which means that \(\left(-\frac{13}{4}, \infty\right)\) is part of the solution.
Solution to the Inequality
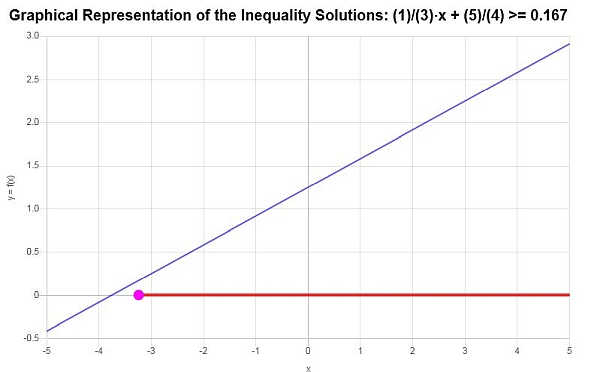
Based on the inequality provided, and analyzing the critical points, we find that the solution to the inequality is: \(x \ge -\frac{13}{4}\).
Using interval notation, the solution is written as:
\[\left[-\frac{13}{4},\infty\right)\]The linear inequality graph of the solution that is obtained is shown below
Example: More inequality examples
Find the solution of the following: \(\sin(x) > 0\)
Solution: We are given the following trigonometric inequality that needs to be solved:
\[\sin\left(x\right) > 0\]Handling an Auxiliary Equation
From the above trig inequality, we obtain the associated equation that we need to be solved first:
\[\sin\left(x\right)=0\]Solving the Auxiliary Trigonometric Equation
so then the solutions are: \(x = \pi{}K\), for an arbitrary integer constant \(K\).
Critical Points Analysis
Based on the solutions to the auxiliary equation, the list of critical points found is: \(\pi{}K\), for an arbitrary integer constant \(K\).
Notice that we have an infinite number of critical intervals, so we analyze some of them below:
• For the interval \(\left(-3\pi{}, -2\pi{}\right)\): The left-hand side is negative, so then \(\left(-3\pi{}, -2\pi{}\right)\) is not part of the solution.
• For the interval \(\left(-2\pi{}, -\pi{}\right)\): The left-hand side is positive, which means that \(\left(-2\pi{}, -\pi{}\right)\) is part of the solution.
• For the interval \(\left(-\pi{}, 0\right)\): The left-hand side is negative, which means that \(\left(-\pi{}, 0\right)\) is not a part of the solution.
• For the interval \(\left(0, \pi{}\right)\): The left-hand side is positive, which means that \(\left(0, \pi{}\right)\) is part of the solution.
• For the interval \(\left(\pi{}, 2\pi{}\right)\): The left-hand side is negative, so then \(\left(\pi{}, 2\pi{}\right)\) is not a part of the solution.
• For the interval \(\left(2\pi{}, 3\pi{}\right)\): The left-hand side is positive, which means that \(\left(2\pi{}, 3\pi{}\right)\) is part of the solution.
And that is how we proceed for the whole sequence of intervals.
Part Solution Intervals
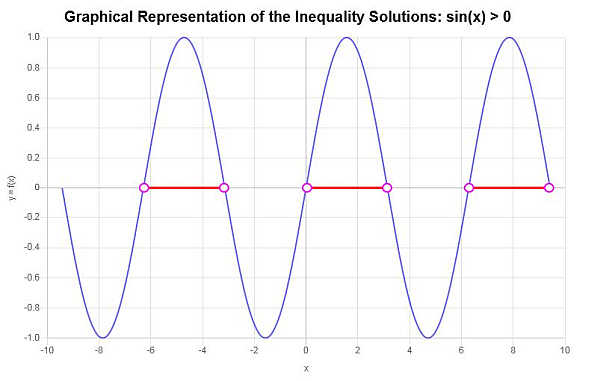
Based on the analysis of the critical points found and the corresponding intervals generated by consecutive critical points, we are able to identify the following as a part of the solution to the inequality:
\[\left(-2\pi{}, -\pi{}\right) \cup \left(0, \pi{}\right) \cup \left(2\pi{}, 3\pi{}\right)\]In this case, we can approximately identify different solution areas, as shown in the graph below. The inequality grapher yields the following graphical depiction of the solution found:
Example: More inequalities
Solve is quadratic inequality \( x^2 - 2x > 6 \).
Solution: The inequality we need to solve is
\[x^2-2x > 6\]Putting all terms of the inequality on one side, we get:
\[x^2-2x-6>0\]Auxiliary Equation
We get the following auxiliary equation, which needs to be solved first:
\[x^2-2x-6=0\]We have a polynomial expression on the left-hand side, which is \(\displaystyle deg(p) = 2\), its leading coefficient is \(\displaystyle a_{2} = 1\) and its constant coefficient is \(\displaystyle a_0 = -6\).
Quadratic Formula
In this case, the roots are computed using the following formula:
\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\] \[\Rightarrow = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(1\right)\left(-6\right)}}{2\cdot 1} = \displaystyle \frac{2 \pm \sqrt{28}}{2}\]so then, we find that:
\[ {x}_1 = \frac{2}{2}-\frac{1}{2}\sqrt{28}=\frac{2}{2}-\sqrt{7}=1-\sqrt{7}=-\sqrt{7}+1 \] \[{x}_2 = \frac{2}{2}+\frac{1}{2}\sqrt{28}=\frac{2}{2}+\sqrt{7}=1+\sqrt{7}=\sqrt{7}+1\]In this case, the quadratic equation \( \displaystyle x^2-2x-6 = 0 \), has two real roots, which become critical points:
Critical Points Analysis
The list of critical points found organized in ascending order is: \(-\sqrt{7}+1\), \(\sqrt{7}+1\).
Based on this, we need to analyze the following intervals:
• For the interval \(\left(-\infty, -\sqrt{7}+1\right)\): The left-hand side is positive, which implies that \(\left(-\infty, -\sqrt{7}+1\right)\) is part of the solution.
• For the interval \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\): The left-hand side is negative, so then \(\left(-\sqrt{7}+1, \sqrt{7}+1\right)\) is not part of the solution.
• For the interval \(\left(\sqrt{7}+1, \infty\right)\): The left-hand side is positive, which means that \(\left(\sqrt{7}+1, \infty\right)\) is a part of the solution.
Finding the solution to the inequality
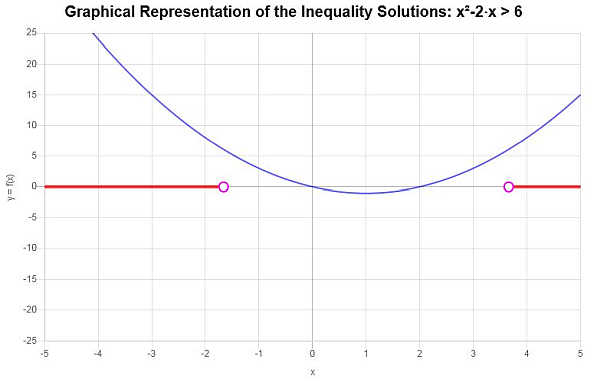
Based on the inequality provided, and analyzing the critical points, we find that the solution to the inequality is: \(x < -\sqrt{7}+1\) or \(x > \sqrt{7}+1\).
Using interval notation, the solution is written as:
\[\left(-\infty,-\sqrt{7}+1\right) \cup \left(\sqrt{7}+1,\infty\right)\]The solution of the inequality shown graphically:
More above inequalities
You will always start with a linear inequalities calculator, or perhaps a quadratic inequalities calculator, because those are the ones guaranteed to render a solution.
Then, even with a polynomial inequality you could be hitting quick sands, as polynomial inequalities can get tricky as well, or even impossibly to solve exactly with elementary methods.
Any other type of inequality will depend on its structure an some clever substitution you could come up with.




