Solving Rational Equations

Using this calculator with steps you will be able to easy work with solving rational equations. The way this works is you simply have to provide a rational equation in the box above. This equation could be as simple as 'x^(1/2) = x^(1/4)', or more complicated than that if you need to.

Then, when you are done typing or pasting the equation you want, you can then click on the "Solve" button, which will solve the equation and will show all the steps of the way.

Rational equations, such as other types of non-linear equations will be in general hard to solve, if you can solve them at all. Usually, only certain rational equations, with certain specific structures will be amenable to being solved explicitly using some standard tricks, like using substitutions.

What is a Rational Equation

A rational equation is one type of equation found in algebra in which at some point in the equation you see a quotient of two polynomials. For example

\[\displaystyle \frac{x}{x+1} + 4 = 1\]

is a rational equation, because of the term \(\frac{x}{x+1} \). Technically, all polynomial equations are also rational equations, because a polynomial can always be considered itself divided by 1, and 1 is a polynomial of order 0 (a constant).

That above is a fancy way of expressing this \(P(x) = \frac{P(x)}{1}\).

Rational Equation Formula

There is not one specific formula for a rational equation, but you should be able to identify them whenever the quotient of two denominators appears in an equation. In terms of a formula, you are trying to identify something like:

\[\displaystyle \frac{P(x)}{Q(x)} \]

somewhere in the equation, in order to classify it as a rational equation.

How to solve rational equations

For example, if you need to solve this rational equation \(\frac{1}{x} + \frac{1}{x^2} = 2\), you could get into the longer way of finding common denominator, which in this case would be \(x^2\) and you would land into a polynomial equation.

But then, you could also do the substitution \(u = \frac{1}{x}\), so then the equation turns into the auxiliary equation \(u + u^2 = 2\), which can immediately be solved using the quadratic equation formula.

Relationship to Rational Expressions

Rational expressions and the simplification of rational expression is a crucial task at the time of solving equations involving rational expressions.

But at the same time, before you run blindly into simplifying and operating the equation at hand, you will want to assess whether or not there is a substitution that will reduce things to a very simple auxiliary equation.

How to Use this Rational Equation Calculator with Steps

The advantage of our calculator is that it will do the calculation showing you the steps, which can certainly come in handy. The main thing is though that not all rational equations will have a solution that we can find using elementary methods.

Solving equations takes a bit of astuteness at times, but will our calculator you will eliminate the guesswork.

Example: A simple rational equation

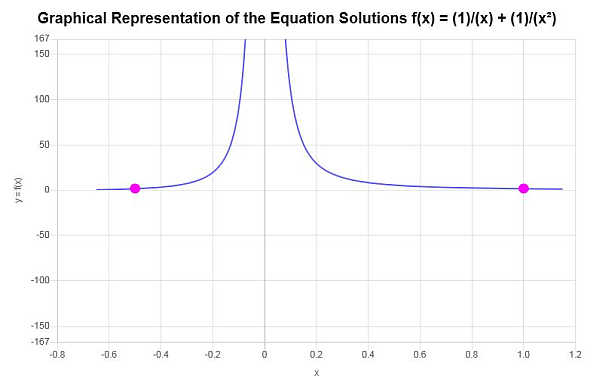
Solve the following equation: \(\frac{1}{x} + \frac{1}{x^2} = 2\)

Solution: We are provided with the following equation

\[\frac{1}{x}+\frac{1}{x^2}=2\]

We use the substitution: \(u = \frac{1}{x}\) so the equation becomes:

\[u + u^2 = 2\]

This quadratic equation can be put as \(u^2 + u - 2 = (u-1)(u+2) = 0\)

which directly leads to the solutions \(u = 1, u = -2\). But since we know that \(u = \frac{1}{x}\), we find the following solution to the original equation:

\[x_1 = -\frac{1}{2} \] \[x_2 = 1 \]

Therefore, solving for \(x\) for the given equation leads to the solutions \(x=-\frac{1}{2},\,\,x=1\).

Graphically

The following is the graphical representation of the solutions obtained:

More equation calculators

Most equation calculators will exploit specific structures in order to try and find and exact solution, but the efforts will not always be successful.

But ultimately, there is not much that can be do in general. The only thing we can do is solve linear equations and solve polynomial equations (to an extent, only quadratic equations are really straightforward to solve).

So then, any strategy for solving an equation has to do with somewhat transforming it using some algebraic reduction into the few types of equations we actually know how to solve. And mostly, all we can do is try some lucky substitutions, if you are lucky enough.