Polynomial Long Division Calculator

This calculator aid with you with the process of conducting a long division between two given polynomials. To this end, you need to provide two valid polynomial expressions. These polynomials maybe already simplified or not, and the calculator will simplify them if they need it.

When dividing polynomials you need to provide two polynomials, one you will be dividing to, which is called the dividend, and the other one is the divisor.

Once you provide two valid polynomials, the next step would be to click on the "Calculate" button, which will show all the corresponding calculation required for the desired long division between the provided polynomials.

The process of conducting a division of polynomials using the Long Division Method is a relatively straightforward method, but which requires an very organized approach, so to not to get lost. Usually, it works best using a tabular approach to be showing the corresponding steps.

A simpler approach is used with synthetic division, but that only applies when the divisor has degree one, so it has a more limited reach

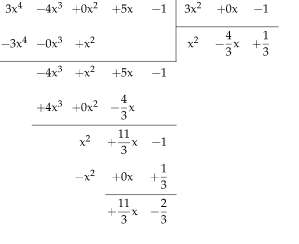
What is a polynomial?

A polynomial is a type of simple expression that combines with sums and subtractions the integer powers of a certain variable x (or whichever variable name is chosen), possibly multiplied by constants.

For example, the expression \(p(x) = 2x^2 + x + 1\) is a combination of the terms \(2x^2\), \(x\) and \(1\) with additions of powers of x (notice that 1 is a power of x, as \(x^0 = 1\).

On the other hand, \(f(x) = 2x^2 + \sin(x) + 1\) is not a polynomial, because the term \(\sin(x)\) is not power of x.

Polynomial Operations

Polynomials, much like numbers, can be operated with addition, subtraction, multiplication and divisions of polynomials. Additions and subtractions are simple to do, in a very intuitive way. For example, if you have two polynomials, \(p(x) = 2x+1\) and \(q(x) = x^3 + 2x+ 3\), adding the polynomial is achieved by literally adding the terms like

\[p(x) + q(x) = 2x + 1 + x^3 + 2x+ 3 = x^3 + 4x + 4\]

For subtractions, you also subtract the corresponding terms of the polynomial that is being subtracted. For example, if you have two polynomials, \(p(x) = 2x+1\) and \(q(x) = x^3 + 2x+ 3\), then, subtracting is done like

\[p(x) - q(x) = 2x + 1 - (x^3 + 2x+ 3) = 2x + 1 - x^3 - 2x - 3) = -x^3 -2\]

Multiplication is more complicated, because you have to cross-multiply terms using the distributive property:

\[p(x) \cdot q(x) = (2x + 1) \cdot (x^3 + 2x+ 3) = 2x \cdot x^3 + 2x \cdot 2x + 2x \cdot 3 + 1\cdot x^3 + 1\cdot1 2x+ 1\cdot 3 = 2x^4 +x^3+4x^2+8x+3\]

Division is slightly more complicated, because it involved the idea that one polynomial may not divide exactly another polynomial. Mathematically, when we have two polynomials \(p(x)\) and \(s(x)\), and we want to divide \(p(x)\) by \(s(x)\), we are looking for a quotient \(q(x)\) and a remainder \(r(x)\) (both of them polynomials), that have the property that \(p(x)= q(x)\cdot s(x) + r(x)\), with the condition that the degree of the polynomial \(r(x)\) is less than the degree of \(s(x)\). This is usually called the Euclid Decomposition.

The Long Division Method

So, the Long Division Method is one systematic way of starting with two polynomials we want to divide \(p(x)\) and \(s(x)\), so we find quotient \(q(x)\) and a remainder \(r(x)\) in such a way that

\[p(x)= q(x)\cdot s(x) + r(x)\]

This algorithm is extremely useful, and though the problem appears simple in appearance, it is not hard to get lost if not using a systematic approach, that is guaranteed to arrive to the required quotient and remainder.

What are the steps for doing a long division?

• Step 1: Identify the two polynomials p(x) and s(x) you want to divide and identify p(x) as the dividend and s(x) as the divisor
• Step 2: Check the degree of the dividend p(x) against the degree of s(x). If the degree of s(x) is greater than the degree of p(x), we have that the remainder is the dividend p(x) itself, and the quotient is zero: q(x) = 0, and you are done
• Step 3: In this case, we assume that the degree of the dividend p(x) is greater than or equal to the degree of the division s(x), otherwise, we would have stopped in step 2
• Step 4: We need to conduct an iterative process of finding a temporary remainder, until we have arrived to remainder that has a degree less than the degree of s(x)
• Step 5: The temporary or interim remainder is updated everytime by first first finding the ratio between the highest term of the current temporary remainder and the divisor s(x). This ratio (which is a power term) multiplies then s(x), and the result of this multiplication is subtracted from the current temporary remainder, leading to an updated remainder
• Step 6: This process continues until the remainder has a degree that is lower than that of s(x). In every step of the iteration, the degree of the temporary remainder is reduced by at least 1, so the process is guaranteed to end

In the end, the process of dividing two polynomials is reduced to compute multiplications are sums of polynomials, which is pretty much what happens with numbers. The long division method for polynomials is the extension of the way we divide numbers to polynomials.

How is Long Division connected with finding roots of a polynomial equation

Assume that p(x) is the dividend you want to divide, and s(x) is the divisor. According to the Long Division method, you will be able to find a quotient q(x) and a remainder r(x) so that:

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

But sometimes, it happens that the remainder is r(x) = 0, and in that case we say that s(x) divides p(x) (or it divides p(x) exactly). So, when r(x) = 0

\[\displaystyle p(x) = q(x)s(x) \]

This indicates that in order to find roots of p(x) = 0, we can get solve q(x) = 0 and s(x) = 0, separately, which are simpler equations to solve.

Advantages of this long division calculator

As I have mentioned before, long division is not too hard, but it does require a systematic approach. A great advantage of using a division calculator like this one is that you will get all the steps of the process shown

It may not be essential to know how to conduct the steps yourself, but this calculator allows you to see how it is done, with each step explaining, removing the mystery of getting the remainder and quotient from, say a digital calculator, which will give you the answer without showing the steps.

A long division calculator with steps showing all the work ensures that you get a clear idea of what is happening with the calculation.

Example: Calculating division of polynomials

Calculate division of the following polynomials: \(p(x) = \frac{1}{3} x^3 + \frac{5}{4}x - \frac{5}{6}\) and \(s(x) = x+3\).

Solution:The following polynomial has been provided: \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\), which needs to be divided by the polynomial \(\displaystyle s(x) = x+3\).

Observe that the degree of the dividend is \(\displaystyle deg(p) = 3\), whereas the degree of the divisor is \(\displaystyle deg(s)) = 1\).

Step 1: The leading term of the dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) is \(\displaystyle \frac{1}{3}x^3\), whereas the leading term for the divisor \(\displaystyle s(x) = x+3\) is equal to \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the dividend is \(\displaystyle \frac{ \frac{1}{3}x^3}{ x} = \frac{1}{3}x^2\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle \frac{1}{3}x^2 \cdot \left(x+3\right) = \frac{1}{3}x^3+x^2\), which we need to subtract to the dividend:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Step 2: In this case, the leading term of the current remainder \(\displaystyle -x^2+\frac{5}{4}x-\frac{5}{6}\) is \(\displaystyle -1x^2\), and we know the leading term for the divisor is \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the of current remainder is \(\displaystyle \frac{ -1x^2}{ x} = -x\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle -x \cdot \left(x+3\right) = -x^2-3x\), which we need to subtract to the current reminder:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Step 3: In this case, the leading term of the current remainder \(\displaystyle \frac{17}{4}x-\frac{5}{6}\) is \(\displaystyle \frac{17}{4}x\), and we know the leading term for the divisor is \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the of current remainder is \(\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}\), which we need to subtract to the current reminder:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

which concludes this calculation, since the degree of the current remainder \(r(x) = -\frac{163}{12}\) is less than the degree of the divisor \(s(x) = x+3\).

Conclusion: Therefore, we conclude that for the given dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) and divisor \(\displaystyle s(x) = x+3\), we get that the quotient is \(\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}\) and the remainder is \(\displaystyle r(x) = -\frac{163}{12}\), and that

\[\displaystyle \frac{p(x)}{s(x)} = \frac{\frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}}{x+3} = \frac{1}{3}x^2-x+\frac{17}{4} - \frac{\frac{163}{12}}{x+3}\]

Example: Polynomial Long Division

Use the long division method to find the remainder and quotient for : \(p(x) = x^4 + x^3 + 2x^2 - \frac{5}{4}x - 2\) and \(s(x) = x^2+1\)

Solution: We have that \(\displaystyle p(x) = x^4+x^3+2x^2-\frac{5}{4}x-2\) needs to be divided by \(\displaystyle s(x) = x^2+1\).

Note the degree of the dividend is \(\displaystyle deg(p) = 4\), and the degree of the divisor is \(\displaystyle deg(s)) = 2\).

Step 1: The term with highest degree of the dividend \(\displaystyle p(x) = x^4+x^3+2x^2-\frac{5}{4}x-2\) is \(\displaystyle x^4\), and the leading term for the divisor \(\displaystyle s(x) = x^2+1\) is equal to \(\displaystyle x^2\).

So then, the term we need to multiply \(x^2\) so to get to the leading term of the dividend is equal to \(\displaystyle \frac{ x^4}{ x^2} = x^2\), which indicates that we need to add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle x^2 \cdot \left(x^2+1\right) = x^4+x^2\), which we need to subtract to the dividend:

\[\begin{array}{rccccc} &\displaystyle x^2 & \displaystyle & \displaystyle &&\\[0.8em] \hline x^2+1\,) & \displaystyle x^4 & \displaystyle +x^3 & \displaystyle +2x^2 & \displaystyle -\frac{5}{4}x & \displaystyle -2\\[0.8em] \displaystyle &\displaystyle -x^4 & \displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle x^3 & \displaystyle +x^2 & \displaystyle -\frac{5}{4}x & \displaystyle -2\\[0.8em] \end{array}\]

Step 2: In this case, the leading term of the current remainder \(\displaystyle x^3+x^2-\frac{5}{4}x-2\) is \(\displaystyle x^3\), and we know the leading term for the divisor is \(\displaystyle x^2\).

So then, the term we need to multiply \(x^2\) to get to the leading term of the of current remainder is \(\displaystyle \frac{ x^3}{ x^2} = x\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle x \cdot \left(x^2+1\right) = x^3+x\), which we need to subtract to the current reminder:

\[\begin{array}{rccccc} &\displaystyle x^2 & \displaystyle +x & \displaystyle &&\\[0.8em] \hline x^2+1\,) & \displaystyle x^4 & \displaystyle +x^3 & \displaystyle +2x^2 & \displaystyle -\frac{5}{4}x & \displaystyle -2\\[0.8em] \displaystyle &\displaystyle -x^4 & \displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle x^3 & \displaystyle +x^2 & \displaystyle -\frac{5}{4}x & \displaystyle -2\\[0.8em] \displaystyle &\displaystyle & \displaystyle -x^3 & \displaystyle & \displaystyle -x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle x^2 & \displaystyle -\frac{9}{4}x & \displaystyle -2\\[0.8em] \end{array}\]

Step 3: In this scenario, the highest degree term of the current remainder \(\displaystyle x^2-\frac{9}{4}x-2\) is \(\displaystyle x^2\), and we know the leading term for the divisor is \(\displaystyle x^2\).

So then, the term we need to multiply \(x^2\) to get to the leading term of the of current remainder is \(\displaystyle \frac{ x^2}{ x^2} = 1\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle 1 \cdot \left(x^2+1\right) = x^2+1\), which we need to subtract to the current reminder:

\[\begin{array}{rccccc} &\displaystyle x^2 & \displaystyle +x & \displaystyle +1&&\\[0.8em] \hline x^2+1\,) & \displaystyle x^4 & \displaystyle +x^3 & \displaystyle +2x^2 & \displaystyle -\frac{5}{4}x & \displaystyle -2\\[0.8em] \displaystyle &\displaystyle -x^4 & \displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle x^3 & \displaystyle +x^2 & \displaystyle -\frac{5}{4}x & \displaystyle -2\\[0.8em] \displaystyle &\displaystyle & \displaystyle -x^3 & \displaystyle & \displaystyle -x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle x^2 & \displaystyle -\frac{9}{4}x & \displaystyle -2\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle -1\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{9}{4}x & \displaystyle -3\\[0.8em] \end{array}\]

and we stop the iteration, since the degree of \(r(x) = -\frac{9}{4}x-3\) (which is 1) is less than the degree of the divisor \(s(x) = x^2+1\).

Conclusion: The conclusion is that for the given dividend \(\displaystyle p(x) = x^4+x^3+2x^2-\frac{5}{4}x-2\) and the provided divisor \(\displaystyle s(x) = x^2+1\), the corresponding quotient is \(\displaystyle q(x) = x^2+x+1\) and the remainder is \(\displaystyle r(x) = -\frac{9}{4}x-3\), and we can relate the polynomials as follows:

\[\displaystyle \frac{p(x)}{s(x)} = \frac{x^4+x^3+2x^2-\frac{5}{4}x-2}{x^2+1} = x^2+x+1 - \frac{\frac{9}{4}x+3}{x^2+1}\]

Example: Find the quotient and remainder

Use long division for \(p(x) = x^3 + x - 1\) and \(s(x) = x-1\).

Solution: The first thing we observe is that the degree of the dividend is \(\displaystyle deg(p) = 3\), and the degree of the divisor is \(\displaystyle deg(s)) = 1\). We carry on the following steps:

Step 1: The leading term of the dividend \(\displaystyle p(x) = x^3+x-1\) is \(\displaystyle x^3\), whereas the leading term for the divisor \(\displaystyle s(x) = x-1\) is equal to \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the dividend is \(\displaystyle \frac{ x^3}{ x} = x^2\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle x^2 \cdot \left(x-1\right) = x^3-x^2\), which we need to subtract to the dividend:

\[\begin{array}{rcccc} &\displaystyle x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x-1\,) & \displaystyle x^3 & \displaystyle & \displaystyle +x & \displaystyle -1\\[0.8em] \displaystyle &\displaystyle -x^3 & \displaystyle +x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +x & \displaystyle -1\\[0.8em] \end{array}\]

Step 2: Now, the leading term of the current remainder \(\displaystyle x^2+x-1\) is \(\displaystyle x^2\), and we know the leading term for the divisor is \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the of current remainder is \(\displaystyle \frac{ x^2}{ x} = x\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle x \cdot \left(x-1\right) = x^2-x\), which we need to subtract to the current reminder:

\[\begin{array}{rcccc} &\displaystyle x^2 & \displaystyle +x & \displaystyle &\\[0.8em] \hline x-1\,) & \displaystyle x^3 & \displaystyle & \displaystyle +x & \displaystyle -1\\[0.8em] \displaystyle &\displaystyle -x^3 & \displaystyle +x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +x & \displaystyle -1\\[0.8em] \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle 2x & \displaystyle -1\\[0.8em] \end{array}\]

Step 3: Now, the leading term of the current remainder \(\displaystyle 2x-1\) is \(\displaystyle 2x\), and we know the leading term for the divisor is \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the of current remainder is \(\displaystyle \frac{ 2x}{ x} = 2\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle 2 \cdot \left(x-1\right) = 2x-2\), which we need to subtract to the current reminder:

\[\begin{array}{rcccc} &\displaystyle x^2 & \displaystyle +x & \displaystyle +2&\\[0.8em] \hline x-1\,) & \displaystyle x^3 & \displaystyle & \displaystyle +x & \displaystyle -1\\[0.8em] \displaystyle &\displaystyle -x^3 & \displaystyle +x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +x & \displaystyle -1\\[0.8em] \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle 2x & \displaystyle -1\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -2x & \displaystyle +2\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle 1\\[0.8em] \end{array}\]

and we stop, because the remainder \(r(x) = 1\) has degree 0, and the divisor \(s(x) = x-1\) has degree 0, so we have reached the point where the remainder has lower degree than the divisor.

Other useful polynomial calculators

Polynomials play a crucial role in algebra, as they are objects that get their derivation from the basic structures that define more advanced concepts such as groups or rings. Dividing polynomials has many useful applications, especially when computing solutions to polynomial equations.

There is one special shortcut that can be taken when the divisor has a degree equal to 1, in which we can use the synthetic division calculator, which greatly simplifies the process of long division, but yet, synthetic division is only used in some specific cases.

Tightly related to polynomials, you will find likely find these simplification calculator useful, as it is normally very convenient to reduce an expression to its lowest before conducting any algebraic operation.