Solving Radical Equations

This radical equation solver allows you to handle radical equations that you provide, by manipulating them algebraically while showing you all the steps of the process.

This solver will accept any valid equation involving roots, such something really simple like 'sqrt(x) = 1', or something that can be a lot harder to solve like 'sqrt(x+3) = x^2 - 1'.

Once a valid radical equation has been provided, you are basically done and all that is left to do is to click on "Solve" so to get all the steps of the process shown .

The solution of radical equation strong relies on effective algebraic manipulation of the expression, in order to basically get rid of the radical part.

What is Radical Equation

A radical equation, put in extremely simple terms, is a type of math equation in which the unknown (typically x) is inside of a radical. For example

\[\displaystyle \sqrt x = x^2 \]

is a radical equation, because of the term \( \sqrt x\), but the equation

\[\displaystyle 2 x = x^2 \]

for example is NOT a radical equation, because we cannot x insider of a radical anywhere in the equation.

How to solve Radical Equations

Solving radical equations is not hard if you follow these steps:

Sometimes, regardless of appropriate grouping and simplification, it won't be possible to eliminate the radicals altogether, or it will lead to an even more complicated equation.

Simplifying Radical Equations

As we mentioned above, the successful calculation of equations involving roots strongly depend on being able to simplify radicals. But sometimes that won't be enough since simplifying all occurring radicals will not make them disappear. The most common way is to reduce radicals and then apply square (power of 2) to cancel the radical.

But squaring to get rid of the radical is a double sword edge, because by squaring any relevant sign could disappear. That is what when "eliminating" the radical and finding solutions of an auxiliary equation, we MUST double check that the auxiliary solutions are also solutions to the original equation. Often times they are not.

Another way to see the process of eliminating the radical is by using a suitable substitution. For example, for the radical equation:

\[\displaystyle \sqrt x = x \]

you may want to set \(u = \sqrt x\), so then \(u^2 = (\sqrt x)^2 = x\), so then the original equation turns into the following auxiliary equation:

\[\displaystyle \sqrt x = x \Rightarrow u = u^2\]

which is a polynomial equation that we can solve. So then, using a substitution leads from an equation we don't know how to solve, to solving a polynomial equation which we do know who to solve.

Why do we care about radical equations?

Radical equations are common appearances in Algebra and Calculus, as they are the basis of modeling so many different phenomena.

Radical functions are interesting in terms of their properties and type of slow growth as x approaches to infinity.

Example: Solving equations involving radical

Solve the following: \(\sqrt{x} = 2x\)

Solution:

We are provided with the following equation. We need to solve this equation that has only one variable, which is \(x\), so the objective is to solve for \(x\):

\[\sqrt{x}=x^2\]

Observe that the degree of the given polynomial is \(\displaystyle deg(p) = 4\), its leading coefficient is \(\displaystyle a_{4} = -1\) and its constant coefficient is \(\displaystyle a_0 = 0\).

Attempting Rational Roots

Rational Roots Candidates: Since the first term with a non-zero coefficient in \(p(x)\) is \(x\), we can factor this term out to get

\[\displaystyle p(x) = -x^4+x = x \left(-x^3+1 \right) \]

but the term in parenthesis has degree that is higher than 2, so there is no elementary formula to factor it. We need to test for possible rational roots.

The next task is to find the integer numbers that divide the leading coefficient \(a_{3}\) and the constant coefficient \(a_0\), that will be used to construct our candidates to be zeroes of the polynomial equation.

Therefore, dividing each divider of the constant coefficient \(a_0 = 1\) by each divider of the leading coefficient \(a_{3} = -1\), we find the following list of candidates to be roots:

\[\pm \frac{ 1}{ 1}\]

Now, all the candidates need to be tested to see if they are a solution. The following is obtained from testing each candidates:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle -\left(-1^3\right)+1 & = & \displaystyle 2 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle -1^3+1 & = & \displaystyle 0 \\\\ \end{array}\]

Polynomial Division: Since we don't have enough roots among the rational candidates, we will divide \(\displaystyle -x^3+1\) by the product of the factors derived from the rational roots, which is \(\displaystyle \left(x-1\right) \).

Step 1: The leading term of the dividend \(\displaystyle p(x) = -x^3+1\) is \(\displaystyle -x^3\), whereas the leading term for the divisor \(\displaystyle s(x) = x-1\) is equal to \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the dividend is \(\displaystyle \frac{ -x^3}{ x} = -x^2\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle -x^2 \cdot \left(x-1\right) = -x^3+x^2\), which we need to subtract to the dividend:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \end{array}\]

Step 2: Now, the leading term of the current remainder \(\displaystyle -x^2+1\) is \(\displaystyle -x^2\), and we know the leading term for the divisor is \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the of current remainder is \(\displaystyle \frac{ -x^2}{ x} = -x\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle -x \cdot \left(x-1\right) = -x^2+x\), which we need to subtract to the current reminder:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle &\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \end{array}\]

Step 3: Now, the leading term of the current remainder \(\displaystyle -x+1\) is \(\displaystyle -x\), and we know the leading term for the divisor is \(\displaystyle x\).

So then, the term we need to multiply \(x\) to get to the leading term of the of current remainder is \(\displaystyle \frac{ -x}{ x} = -1\), so we add this term to the quotient. Also, we multiply this by the divisor to get \(\displaystyle -1 \cdot \left(x-1\right) = -x+1\), which we need to subtract to the current reminder:

\[\def\arraystretch{1.5}\begin{array}{rcccc} &\displaystyle -x^2 & \displaystyle -x & \displaystyle -1&\\[0.3em] \hline x-1\,) & \displaystyle -x^3 & \displaystyle & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle -x & \displaystyle \\[0.3em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle -x & \displaystyle +1\\[0.3em] \displaystyle &\displaystyle & \displaystyle & \displaystyle x & \displaystyle -1\\[0.3em] \hline \displaystyle & & & & 0\\[0.3em] \end{array}\]

Therefore, the quotient is \(\displaystyle q(x) = -x^2-x-1\), and the remainder is \(\displaystyle r(x) = 0\).

So after dividing, we have advanced in the factorization with

\[\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\]

But now, since the quotient found \(\displaystyle -x^2-x-1\) is quadratic, we can find its roots to see if we can factor it on the real field.

We need to solve the following given quadratic equation \(\displaystyle -x^2-x-1=0\).

Using the Quadratic Formula

For a quadratic equation of the form \(a x^2 + bx + c = 0\), the roots are computed using the following formula:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In this case, we have that the equation we need to solve is \(\displaystyle -x^2-x-1 = 0\), which implies that corresponding coefficients are:

\[a = -1\] \[b = -1\] \[c = -1\] \[\Delta = b^2 - 4ac = \displaystyle \left( -1\right)^2 - 4 \cdot \left(-1\right)\cdot \left(-1\right) = -3\]

Since in this case we get the discriminant is \(\Delta = \displaystyle -3 < 0\), which is negative, we know that the given equation has two different conjugate complex roots.

Now, plugging these values into the formula for the roots we get:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{1 \pm \sqrt{\left(-1\right)^2-4\left(-1\right)\left(-1\right)}}{2\cdot -1} = \displaystyle \frac{1 \pm \sqrt{-3}}{-2}\]

so then, we find that:

\[\displaystyle {x}_1 = \frac{1 - i \sqrt{3}}{-2} = -\frac{1}{2}+\frac{1}{2}\sqrt{3}i\] \[\displaystyle {x}_2 = \frac{1 + i \sqrt{3}}{-2} = -\frac{1}{2}-\frac{1}{2}\sqrt{3}i\]

So after finding the roots of the last quadratic part, we find two complex roots, so we cannot factor the term \(-x^2-x-1\) in the real field, so we end the process with \(\displaystyle p(x) = -x^4+x = - x \left(x-1\right) \left(-x^2-x-1\right)\).

Therefore, solving for \(x\) for the given polynomial equation leads to the solutions \(x = \, \)\(0\), \(1\), \(-\frac{1}{2}+\frac{1}{2}\sqrt{3}i\), \(-\frac{1}{2}-\frac{1}{2}\sqrt{3}i\), using factorization mathods.

Checking the Auxiliary Solutions

Testing these solutions from the auxiliary polynomial equation shows that not all the candidate solutions are in fact a solution of the original equation. The only actual solutions to the original equation are:

\[x_1=0 \]
\[x_2=1 \]

Therefore, solving for \(x\) for the given equation leads to the solutions \(x=0,\,\,x=1\).

Graphically

The following is the graphical representation of the solutions obtained:

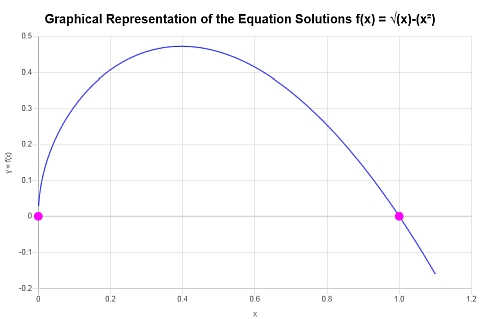
which concludes the calculation.

Other useful equation solvers

When solving radical equations, unlike the case of when you need to solve linear equations or when you need to solve a quadratic equation, falls into thee category of those equations that require so clever algebraic manipulation in order to solve for x.

In other words, you won't have a "do it this way and it will always work" type thing. The type of manipulation you conduct will depend on the structure of the equation, and can greatly vary from case to case.

Simplifying expressions first is always a good practice, because you will reduce terms that may be cluttering the overall structure of the equation.