Logarithmic Function Calculator
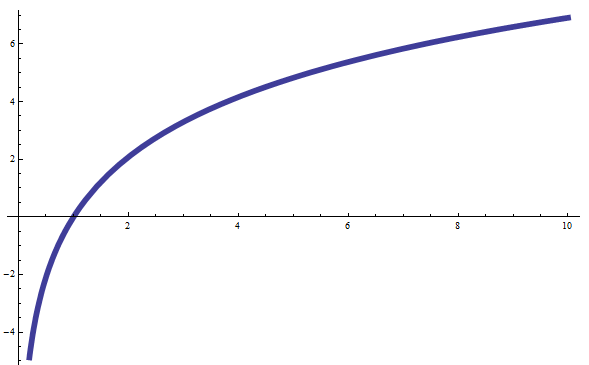
Instructions: Use this step-by-step Logarithmic Function Calculator, to find the logarithmic function that passes through two given points in the plane XY. You need to provide the points \((t_1, y_1)\) and \((t_2, y_2)\), and this calculator will estimate the appropriate exponential function and will provide its graph.
Logarithmic Function Calculator from Two Points
The main purpose of this calculator is to estimate the parameters \(A_0\) and \(k\) for the logarithmic function \(f(t)\) which is defined as:
\[f(t) = A_0 \ln(k t)\]The parameters need to be so the logarithmic function passes through the two given points \((t_1, y_1)\) and \((t_2, y_2)\).
How do you estimate a logarithmic function from two points?
Algebraically speaking, you need to solve the following system of equations to find the parameters \(A_0\) and \(k\):
\[y_1 = A_0 \ln(k t_1)\] \[y_2 = A_0 \ln(k t_2)\]By solving this system for the unknowns \(A_0\) and \(k\), we can find unique solutions, as long as \(t_1 \ne t_2\).
Indeed, by subtracting both sides of the equations:
\[\displaystyle y_1 - y_2 = A_0 \left( \ln(k t_1) - \ln(k t_2) \right)\] \[\displaystyle \Rightarrow \, y_1 - y_2 = A_0 \ln \left(\displaystyle\frac{k t_1}{k t_2}\right) \] \[\displaystyle \Rightarrow \, y_1 - y_2 = A_0 \ln \left(\displaystyle\frac{t_1}{t_2}\right) \] \[ \Rightarrow \, A_0 = \displaystyle \frac{y_1 - y_2}{\ln(t_1) - \ln(t_2)} \]which solves the equations for \(A_0\). Now, in order to solve for \(k\) we use the first equation and apply exponential to both sides::
\[y_1 = A_0 \ln(k t_1)\] \[ \Rightarrow \, \displaystyle e^{\frac{y_1}{A_0}} = k t_1 \] \[ \Rightarrow \, k = \displaystyle \frac{e^{\frac{y_1}{A_0}}}{t_1} \]and there we have found \(k\), as function of \(A_0\) that is already determined and known.
How do you calculate an exponential function?
If instead of a logarithmic function you are interested in exponential behavior, then you should probably use this exponential function calculator , which follows the same logic of estimating parameters to enforce the function passing through two given points.