Calculator of Percentages

This percentage calculator gives you a quick way of conducting the operation you need by simply typing the numbers you need and clicking on the calculate button

Now if you want to do it manually, the calculation of what percentage a number \(D\) is of another number \(X\) is quite simple, and involves some elementary operations.

How Do You Compute a Percentage? The Percentage Formula

Students frequently ask "How do I calculate a percent", and the answer is quite simple. We compute the required percentage by simply using the following formula:

\[\text{Percentage} = \displaystyle\frac{D}{X} \times 100\]

Simple as that. You take the value of the number \(D\) and you divide it by \(X\). Then, the result of that division you multiply by 100 and you get the desired percentage.

In other words, you have a part (D) divided by the total (X). Multiplying by 100 has the effect of normalizing the output, so that the percentage of the total with respect to itself is 100%.

Steps for Calculating a percent

• Step 1: Identify clearly the part (D) and the total (X) you are working with
• Step 2: If these amounts have units (meters, ounces, etc), make sure you use a common unit for them
• Step 3: You simply compute the percentage by using the following formula: \(\text{Percentage} = \displaystyle\frac{D}{X} \times 100\)

Observe that if the amounts have units, you must make use of a common unit. For example, if I ask you "What percentage is 30 cms of 2 meters?", then we could say that the part is X = 30, and the total is D = 2, and then inadvertently we can compute percentage as \(\text{Percentage} = \displaystyle\frac{30}{2} \times 100 = 1500 %\).

What is wrong with that calculation? The units, they are using different units. Using centimeters for both, we have that the part is 30 centimeters and the total is 2 meters, or 200 centimeters. So the actual percentage is \(\text{Percentage} = \displaystyle\frac{30}{200} \times 100 = 15 %\).

How do I calculate a percentage between two numbers?

Like we explained in the previous part, you need to divide the part (D) by the total (X). Now, when you have two numbers, then one of them plays the role of the part and the other is the total.

In other words, when you have two numbers, you compute the percentage of one number relative to the other, and the order you choose matters. This is, when you have two numbers \(A\) and \(B\), one thing is the percentage of \(A\) with respect to \(B\) which is not the same as the percentage of \(B\) with respect to \(A\)

What is 15 percent as a number? One practical application

From the percentage calculator formula, we first do a division and after that we multiply by 100. Then, reversely, to get 15 percent as a number, we need to divide 15 by 100, so then, 15 percent = 0.15.

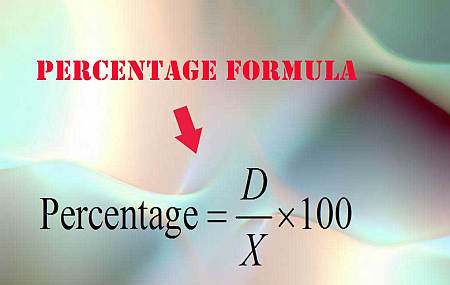
How do you work out 40% of 80?

Very similar to the previous part. In order to work out a percentage of a number, we write the percentage as a number. In this case, 40 percent is the same as 40/100 = 0.40 as a number.

Then, in order to get 40% of 80, we just multiply 0.40*80 = 32. This rationale would apply to all problems of the same type. For example, for 15% of 100 we get that 15% as a number is equal to 15/100 = 0.15, so then 15% of 100 is 0.15*100 = 15.

How to calculate percentage of a number

The steps to calculate the percentage of a number are simple:

• Step 1: Identify clearly the number X, and the percentage p% you want to computer
• Step 2: Now, you need to convert the percentage into a number, and for that you divide p by 100. For example, if p = 85%, then you get p = 85/100 = 0.85
• Step 3: Finally, the percentage of the number you are looking for is simple obtained by multiplying p (as a number) by the number, so this is p*X

Example of a percentage calculator

Example: What percentage is 13 of 38?

Using the above formula, we get:

\[\text{Percentage} = \displaystyle\frac{13}{38} \times 100\] \[ = 0.342105263 \times 100\] \[ = 34.21 \%\]

Is This Related to a Fraction to Percentage Calculator?

Absolutely, this is related to computing fraction to percentage . In a way, it is the same thing. Indeed, in this case, all we are doing is checking what is the fraction \(\frac{D}{X}\) as a percentage.

Or in other words, compute what percentage is \(D\) of \(X\) is the same as computing what percentage corresponds to the fraction \(\frac{D}{X}\).