Derivative Calculator

This derivative calculator will take you through all the steps and rules used to find the derivative of a given function. You have to type in a function like 3x + sin(x^2), or you can actually preface it with the whole function definition, like f(x) = 3x^ 2 + 2tan(x^3).

Notice that this can be referred to as a first derivative calculator the same as a derivative calculator. First derivative and derivative represent the same thing, and the "first" part is usually dropped.

The function provided may come fully simplified or not, it does not matter, as the calculator will first simplify the function if necessary before calculating its derivative.

Once a valid function has been provided, you just need to click on "Calculate", wait a few seconds, and all the steps of the calculation will be presented to you.

Differentiation is the main tool used in Calculus (along with integration) and it is a crucial operation that is broadly used in more advanced Math. Some very common applications include tangent line calculation, maxima and minima and a lot more.

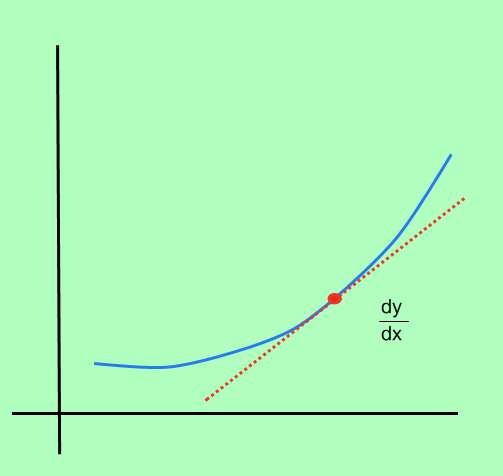
How to calculate the derivative of a function?

The process of computing the derivative of a function is called differentiation, and it consists of determining the instant rate of change of the point, at every point in the domain of the function.

What is the instant rate of change of a function? Well, let's start with the definition of rate of change: Consider a function \(f\), and assume that we have two points, \(x_0\) and \(x_1\). At the point \(x_0\), the function is \(f(x_0)\), and at the point \(x_1\), the function takes the value \(f(x_1)\)

Then, the change in f is defined as \(\Delta y = f(x_1) - f(x_0)\) (which is also referred as the change in y). Also, the change in x is defined as \(\Delta x = x_1 - x_0)\). In simple words, \(\Delta x\) is the change in x, whereas \(\Delta y\) is the change in the value of the function, due to the change in x.

Graphically:

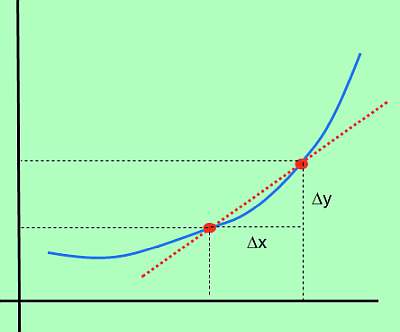
Derivative Formula

So, if \(\Delta x\) represents the change in x, and\(\Delta y\) represents the change in the value of the function, due to the change in x, the corresponding rate of change is:

\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]

So then, what would be the instant rate of change? That would corresponds to analyzing what would happen if \(\Delta x\) becomes really small. One would expect that \(\Delta y\) would also become small, but that would happen to the rate between \(\Delta y\) and \(\Delta x\)?

So, in this context, the instant rate of change is defined as

\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]

So, in layman terms, we set \(x_0\) fixed and we compute the rate of change for values of \(x_1\) that are closer and closer to \(x_0\). Using this idea of instant rate of change, we can give the following formula for the derivative at a point \(x_0\).

\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]

If the above limit exits, we say that the function f is differentiable at \(x_0\). Also, we will say that a function is differentiable at a set A, if the function is differentiable at every point of the set.

Steps for using the derivative formula

• Step 1: Identify clearly the function f you want to differentiate
• Step 2: Make sure you simplify f as much as possible, otherwise finding the required limit may be unnecessarily harder
• Step 3: Decide whether you will work with a generic point x0, or you are giving a specific numeric point for x0
• Step 4: Based on the definition of the function, use the formula \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \). This is, plug the values of x0 and x1 in f, and see how does the formula looks algebraically
• Step 5: Simplify as much as you can BEFORE taking the limit
• Step 6: Sometimes it easier to set x1 = x0 + h, and then compute the limit as h converges to 0

Notice that Step 6 is one that some people like as the default. Indeed, the alternative derivative formula that may seem easier for simplification purposes is:

\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]

which is the formula that you may find in your textbook, instead of the other one.

Derivative Rules

It would seem like a heck lot of work to compute the derivative using the formula. And indeed, it could be a laborious process if we decided to work out every differentiation process using the derivative formula.

Fortunately, there are a number of functions (namely polynomials, trigonometric functions) for which we know with precision what their derivative are.

On top of that, we have differentiation rules that allow us to find the derivative of a function that is a composite function and/or a combination of elementary functions (for which we know their derivative), in terms of elementary derivatives.

What are steps for calculating the derivative?

• Step 1: Identify function f you want to differentiate. Simplify as much as you can BEFORE calculating its derivative
• Step 2: Determine whether or not you are required to use the derivative formula or not
• Step 3: If you must use the derivative formula, use \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \), or you can use \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \) if it seems easier to approach
• Step 4: If you are not required to use the derivative formula, you can use the main differentiation rules: Linearity, Product Rule, Quotient Rule and Chain Rule, which will help you to reduce the calculation of the derivative to using basic known derivatives

Often times, the function you are trying to find the derivative for is not a simple function, but it is basic combination of several simple functions. For example, the function

\[f(x) = x + \cos(x) + \sin(x)\]

is not an elementary function in itself, but it is composite function of three elementary functions, \(x\), \(\sin x\) and \(\cos x\).

Applications of Derivatives

One could think "well, derivatives involve limits and that is super theoretical, so then it must not have too many applications", but you would be completely wrong. The magic of derivatives is that they are essentially about the rate of change of functions, that can represent different types of processes.

That is why differentiation allows to study the process of change, and how to compare changing variables, which has a broad applicability.

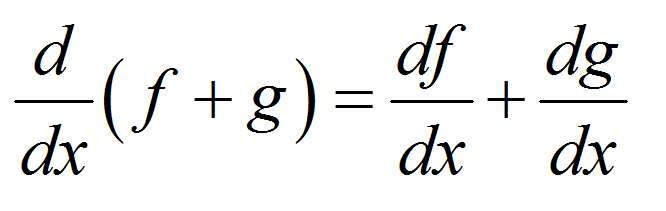
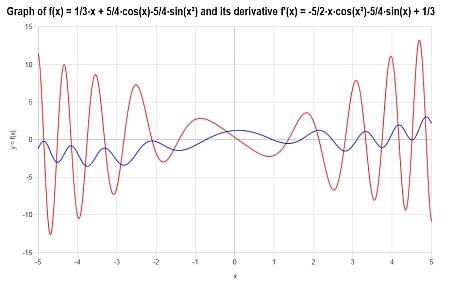
Example: Calculating the derivative

Calculate the derivative with respect to x for \(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)

Solution:The following function has been provided: \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), for which we need to compute its derivative.

Initial Step: In this case, we first need to simplify the given function \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \), and in order to do so, we conduct the following simplification steps:

After simplifying the function, we can proceed to the calculation of the derivative:

The following plot is obtained for \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\) on the interval \([-5, 5]\):

Example: Differentiating a function

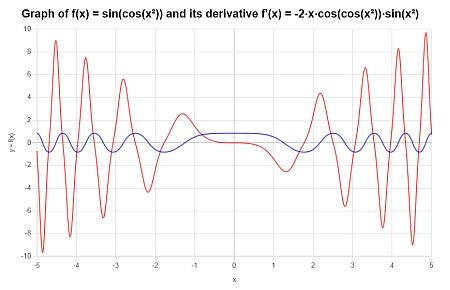
Calculate the derivative of : \(f(x) = \sin(\cos(x^2))\), and provide the graph of \(f(x)\) and \(f'(x)\).

Solution: Now we have \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\).

The function came already simplified, so we can proceed directly to compute its derivative. By using this derivative cal we get:

Therefore, we get the following plot for the function on the interval \([-5, 5]\):

Example: Derivative calculator

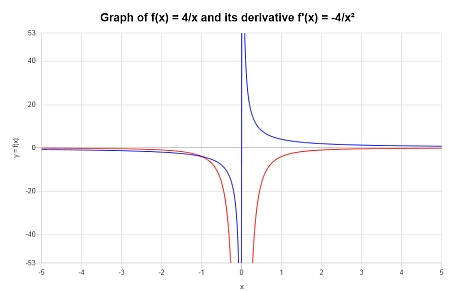
Find the derivative of \( f(x) = \displaystyle \frac{4}{x}\). Is it well defined everywhere? Graph it.

Solution: The function provided for which the derivate is needed is \(\displaystyle f(x)=\frac{4}{x}\).

There is no further simplification needed, so we can proceed directly to compute its derivative:

Graphically:

More about derivatives and functions

This derivative calculator with steps will prove very useful to you as it will conduct the calculation of the derivative of any given function, showing all the steps of the process, applying the appropriate derivative rules, and telling you when they are being applied and why.

This calculator can also be called dy dx calculator or differential quotient calculator as that is precisely what it does, it computes the limit of the dy/dx ratio as dx approaches to 0.

Functions are extremely important constructs in Math. Along with differentiation, you need to be able to simplify a function usually, as a preamble of other more specialized calculations. There are special types of functions that allow you to conduct specific operations, such as what you do with polynomial operations.

Interestingly, lots of important elements like finding the coordinates of the vertex of a parabola that can be derived in a clever way using geometric arguments, can be trivially obtained using differentiation.

Also, the idea of tangent line and first order approximation appear naturally, stemming out from the concept of derivative, and a natural extension.