Z-Score to Percentile Calculator
Instructions: This Z-Score to Percentile Calculator will compute the percentile associated to a Z-score that is provided by you, and a graph will be shown to represent this percentile. Please provide the information required below:
How Do You Compute a Percentile from a Z-Score?
A Z-scores is a normalized score that will allow you to compare values relative to their population. This is, if you have two different students who tool different tests, in principle those scores have different scales and cannot be compared. But by converting the tests scores into z-scores (by normalizing them), we can put them in the same scale, if you will.
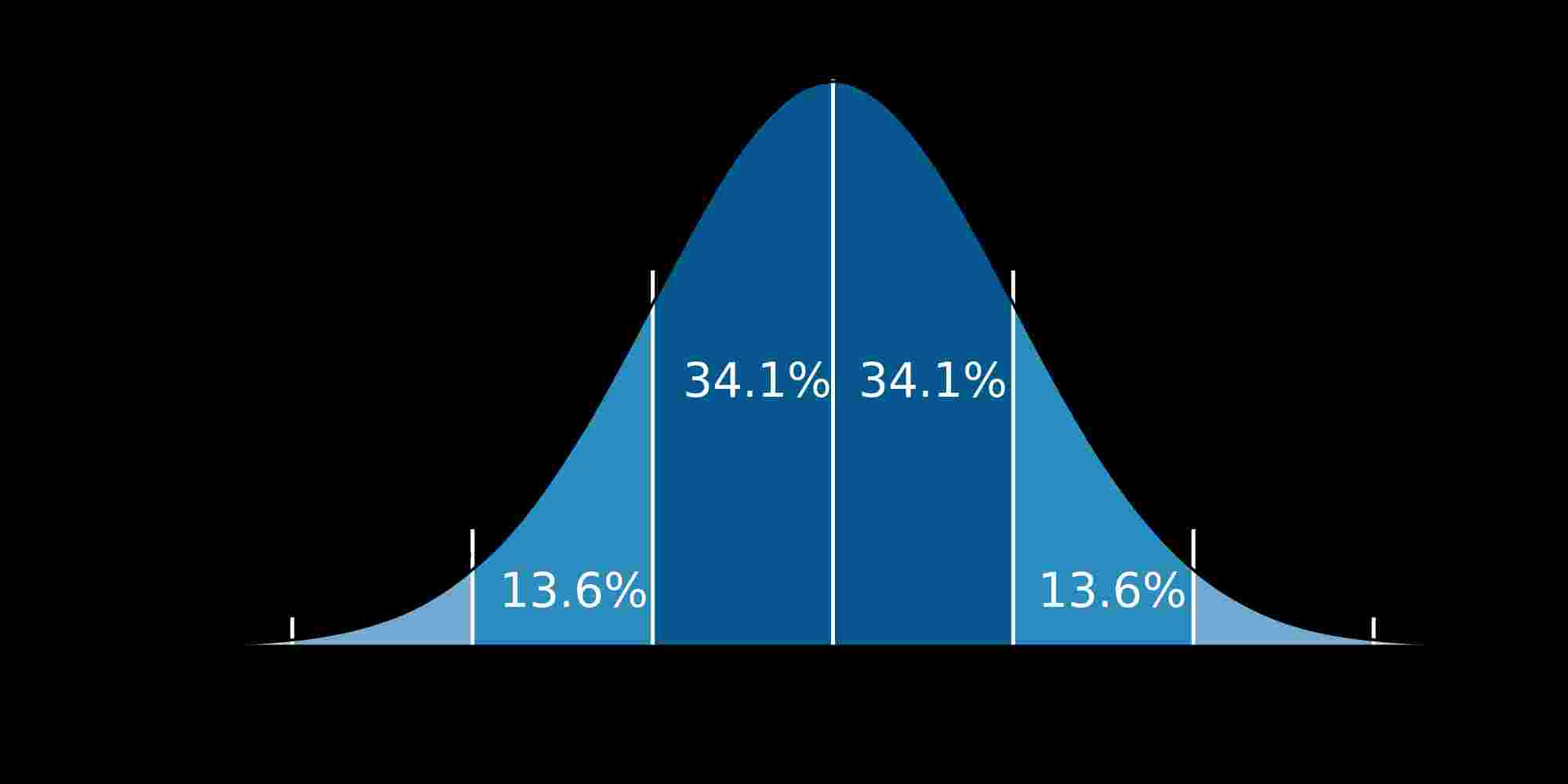
Also, a z-score represents a specific location in the distribution, so that there is a certain area that is to the left of that z-score. And that's exactly how we define the percentile associated to a z-score: it is the area (in percentage terms) that is to the left of that z-score.
Mathematically, for a given z-score \(z\), we compute
\[ p = \Pr(Z < z) \]Then, given that probability \(p\), we say that the z-score \(z\) is associated to the \(100\cdot p \%\) percentile.
Say that you have a percentile instead, what you should use is this percentile to z-score . On the other hand, if what you need to compute probabilities instead, use our normal distribution calculator . Also, you can use our z-scores calculator or our calculator that normalizes a sample of data .