Poisson Distribution Calculator
Instructions: Compute Poisson distribution probabilities using the form below. Please type the population mean (λ), and provide details about the event you want to compute the probability for:
Poisson Probability Calculator
More about the Poisson distribution probability so you can better use the Poisson calculator above: The Poisson probability is a type of discrete probability distribution that can take random values on the range \([0, +\infty)\). The main properties of the Poisson distribution are:
- It is discrete, and it can take values from 0 to \(+\infty\).
- The type of skewness depends on the population mean (\(\lambda\))
- It is determined by the population mean (\(\lambda\))
- Its mean is \(\lambda\) and its population variance is also \(\lambda\)
How to use the Poisson distribution calculator
Using the above Poisson distribution curve calculator , you are able to compute probabilities of the form \(\Pr(a \le X \le b)\), of the form \(\Pr(X \le b)\) or of the form \(\Pr(X \ge a)\).
Type the appropriate parameter for \(\lambda\) in the text box above, select the type of tails, specify your event and compute your Poisson probability. Observe that \(\lambda\) corresponds to the population mean of the distribution.
How do you calculate Poisson probability?
The Poisson probability distribution formula is
\[ \Pr(X = k) = \displaystyle \frac{e^{-\lambda} \lambda^k}{k!}\]There is no simple or short expression to express the Poisson cdf formula, which is obtaining by adding the individual probability values up to a certain given threshold value.
How do you find Poisson probability between two numbers?
Essentially, you need to evaluate the cumulative (cdf) poisson formula at the end points, which would be the two numbers, say k and m. But since the distribution is discrete, what you compute is F(m) - F(k-1), where F is the Poisson cdf function.
Now, if you use our calculator, you don't have to worry about that, and just provide the two numbers in the form above.
How to calculate the Poisson distribution Calculator Excel
Excel has a formula, the "=POISSON()" formula that allows to get either the pdf or the cdf of Poisson.
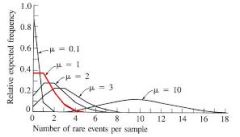
Is there any difference between the Poisson and the Binomial Distribution?
Yes, there are clear differences. First off, they are not the same distribution. Although they are both discrete (take values that can be numerated, like 0, 1, 3, 4, etc), they have some fundamental differences.
For example, the Poisson distribution is determined by one parameter only, which is its mean \(\lambda\). On the other hand, the binomial distribution requires of a sample size N, and the probability of success.
One interesting similarity is that both the Poisson and Binomial probability distributions can be tightly approximated with the normal distribution under certain circumstances (sample size sufficiently large).
Indeed, you can check that out with our normal approximation for the binomial and normal approximation for the Poisson distribution.
Advantages of this Poisson calculator
- Although Excel can aid you with most of your Stats calculation, this calculator shows you all the steps
- By seeing the steps, you can better understand the process of the calculation of probabilities
- Ultimately, all discrete distribution follow the same rationale to compute probabilities
Example: Uses of this Poisson distribution probability calculator
Question: Suppose that a variable X has a Poisson distribution with mean 3.4. Find the following probability: \(\Pr(3 \le X \le 6)\).
Solution:
We need to compute a binomial distribution probability. The following information are provided:
| Population Mean \((\lambda)\) = | \(3.4\) |
| Probability Event = | \(\Pr(3 \le X \le 6) \) |
We need to compute \(\Pr(3 \le X \le 6)\). Therefore, the following is obtained:
\[ \Pr(3 \le X \le 6) = \sum_{i=3}^{ 6} {\Pr(X = i)} = \Pr(X = 3) + \Pr(X = 4) + \Pr(X = 5) + \Pr(X = 6) \] \[ = 0.2186 + 0.1858 + 0.1264 + 0.0716 \]\[= 0.6024 \]which completes the calculation.
Other discrete probability distribution calculator
This Poisson distribution calculator with steps corresponds to a solver for a discrete distribution. We have other discrete distribution calculators that you may be interested in, such as our Binomial distribution calculator , Geometric distribution calculator , and Hypergeometric distribution calculator , to mention a few of them.
Also, you can use our general discrete probability calculator which will provide you with the mean and standard deviation of a generic discrete distribution.