Polynomial Zeros

This calculator will allow you compute polynomial roots of any valid polynomial you provide. This polynomial can be any polynomial of degree 1 or higher.

For example, you can provide a cubic polynomial, such as p(x) = x^3 + 2x^2 - x + 1, or you can provide a polynomial with non-integer coefficients, such as p(x) = x^3 - 13/12 x^2 + 3/8 x - 1/24.

Once you have provided the calculator with a valid polynomial for which you want to compute its roots, you can click on the "Calculate" button, and you will see a step-by-step run of the process.

It needs be mentioned that the process only involve elementary methods used to find roots, which includes the rational zero theorem and polynomial division, as well as using the quadratic formula when appropriate.

There is no general method to find ALL the roots for ALL possible polynomials of degree above 5, so this calculator will only find roots that can be obtained with these mentioned elementary methods.

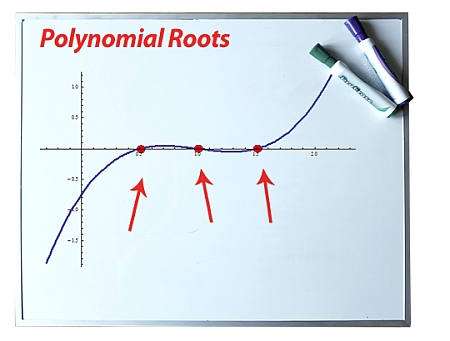
What is the root of a polynomial?

Given a polynomial function \(p(x)\), we say that \(x\) is a root of the polynomial if:

\[\displaystyle p(x) = 0 \]

In layman terms roots of a polynomial are the points the the polynomial function \(p(x)\) crosses the x-axis. That's a good representation to get an idea, but it is not completely precise because some roots could be complex numbers. So then, a real root will be a point where \(p(x)\).

Observe that the roots of the polynomial are also called polynomial zeros.

What are the steps for finding the zeros of a polynomial?

• Step 1: Identify expression you want to work with. Make sure it is a polynomial and simplify as much as possible
• Step 2: We will use the polynomial factoring approach to find its root
• Step 3: Start trying to find elementary (rational) roots with the rational zero theorem, and use polynomial division to reduce the original polynomial, if possible
• Step 4: If Step 3 worked and you could reduce the original polynomial, repeat the previous steps to try to factor the reduced polynomial

It is usually not easy, and it can be computationally intensive, and it is not guaranteed to work, but it is the best possible approach if we are restricted to using elementary methods.

Is factoring the only way to find roots

Not really, but things go hand-to-hand. The factor theorem states that \(x - a\) is a factor of a polynomial \(p(x)\) if and only if \(p(a) = 0\). So in other words, roots and factors are intimately linked.

Now, for polynomials of degree 2 (this is, quadratic polynomials) we can use an explicit formula, which is the well know quadratic formula.

The same happens for degrees 3 and 4, though the formulas are far from elementary. But for degree 5 and higher, there is no such formula, a key result proven by Galois and Abel. So there is no hope to find a "general formula", and which is why the use a more lax polynomial factorization approach.

Common mistakes to avoid

Often times students get frustrated that they cannot find the roots of a given polynomial function, say \(p(x) = x^3+2 x^2-x+1 \), but they need to face the fact that not all polynomials will be able to be solved using elementary tools.

Granted, there is a formula to solve \(x^3+2 x^2-x+1 = 0 \), but it is not elementary, and it is not expected that students know it.

Tips for success

Always try to do a mental map of what your strategy will be: Take note of the polynomial you have, its degree, its leading coefficient and constant coefficient.

Plot the polynomial if you can, to get an idea of its behavior. Are there any obvious factorization that you can use? Use them. Always remember factors = roots.

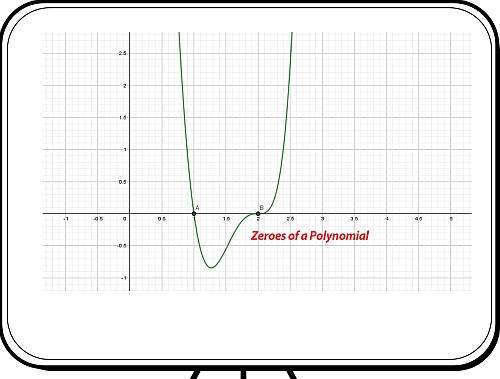
Example: Zeros of a Polynomial

What are the zeros of : \(x^5 + x^4 - x^3 + x^2 - x + 1\)?

Solution: For this example we are provided with the following polynomial: \(\displaystyle p(x) = x^5+x^4-x^3+x^2-x+1\). We will use the factoring approach to finding roots.

Simplification not needed: The provided polynomial expression is simplified already, so there is nothing to simplify it further.

It can be noted that the degree of the provided polynomial is \(\displaystyle deg(p) = 5\). Also, its leading coefficient is \(\displaystyle a_{5} = 1\) and its constant coefficient is equal to\(\displaystyle a_0 = 1\).

Now we search for integer numbers that divide the leading coefficient \(a_{5}\) and the constant coefficient \(a_0\), which is used to find rational candidates .

▹ The dividers of \(a_{5} = 1\) are: \(\pm 1\).

▹ The dividers of \(a_0 = 1\) are: \(\pm 1\).

Therefore, dividing all factors of the constant term \(a_0 = 1\) by all the dividers of \(a_{5} = 1\), we get the following list of potential roots:

\[\pm \frac{ 1}{ 1}\]

Now, all potential solutions must be evaluated. The results obtained from testing each candidate are as follows:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle \left(-1\right)^5+\left(-1\right)^4-\left(-1\right)^3+\left(-1\right)^2-\left(-1\right)+1 & = & \displaystyle 4 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^5+1^4-1^3+1^2-1+1 & = & \displaystyle 2 \ne 0 \\\\ \end{array}\]

Since no rational roots were identified through manual inspection, further simplification using basic techniques is not possible and the process ends with this step.

Conclusion: As a result, no simplification was obtained and no roots of the polynomial were identified through basic techniques

Example: Calculating roots a quadratic function

Calculate the solutions of: \(3x^2 - 2x - 4 = 0\).

Solution: We need to solve the given quadratic equation \(\displaystyle 3x^2-2x-4=0\).

The roots for a quadratic equation of the form \(a x^2 + bx + c = 0\) are calculated using the following equation:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

In this context, the equation that needs to be solved is \(\displaystyle 3x^2-2x-4 = 0\), indicating that the corresponding coefficients are:

\[a = 3\] \[b = -2\] \[c = -4\]

First, we will determine the nature of the roots by calculating the discriminant. The discriminant is calculated as follows:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(3\right)\cdot \left(-4\right) = 52\]

Since in this case we get the discriminant is \(\Delta = \displaystyle 52 > 0\), which is positive, so then, the equation has two different real roots.

From this we get:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(3\right)\left(-4\right)}}{2\cdot 3} = \displaystyle \frac{2 \pm \sqrt{52}}{6}\]

so then, we find that:

\[ x_1 = \frac{2}{6}-\frac{1}{6}\sqrt{52}=\frac{2}{6}-\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}-\frac{1}{3}\sqrt{13}=\frac{1}{3}-\frac{1}{3}\sqrt{13} \] \[x_2 = \frac{2}{6}+\frac{1}{6}\sqrt{52}=\frac{2}{6}+\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}+\frac{1}{3}\sqrt{13}=\frac{1}{3}+\frac{1}{3}\sqrt{13}\]

We find that the equation \( \displaystyle 3x^2-2x-4 = 0 \), has two real roots, so then:

\[\displaystyle 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

so then the original polynomial is factored as \(\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right) \), which completes the factorization.

Conclusion: Therefore, the factorization we get looking for is given by:

\[\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

The roots found are \(-\frac{1}{3}\sqrt{13}+\frac{1}{3}\) and \(\frac{1}{3}\sqrt{13}+\frac{1}{3}\) .

Example: Polynomial Zeros

Calculate the zeros of the following polynomial: \(p(x)= x^3 - \frac{13}{12} x^2 + \frac{3}{8} x - \frac{1}{24} \).

Solution: Finally, in this example we have: \(\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24}\).

First Step: The provided polynomial expression is irreducible, so there is nothing to simplify. We can proceed to factor it.

Observe that the degree of the given polynomial is \(\displaystyle deg(p) = 3\), its leading coefficient is \(\displaystyle a_{3} = 1\) and its constant coefficient is \(\displaystyle a_0 = -\frac{1}{24}\).

Rational Roots: We will try to find simple rational roots first, with the Rational Zero Theorem.

The next task is to find the integer numbers that divide the leading coefficient \(a_{3}\) and the constant coefficient \(a_0\), that will be used to construct our candidates to be zeroes of the polynomial equation.

Note: In this case, we observe that in order to have both constant and leading coefficient we need to amplify both sides of the equation by \(24\). The equivalent equation is:

\[24x^3-26x^2+9x-1 = 0\]

▹ The dividers of \(a_{3} = 24\) are: \(\pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 8,\pm 12,\pm 24\).

▹ The dividers of \(a_0 = -1\) are: \(\pm 1\).

Therefore, dividing each divider of the constant coefficient \(a_0 = -1\) by each divider of the leading coefficient \(a_{3} = 24\), we find the following list of candidates to be roots:

\[\pm \frac{ 1}{ 1},\pm \frac{ 1}{ 2},\pm \frac{ 1}{ 3},\pm \frac{ 1}{ 4},\pm \frac{ 1}{ 6},\pm \frac{ 1}{ 8},\pm \frac{ 1}{ 12},\pm \frac{ 1}{ 24}\]

Now, all the candidates need to be tested to see if they are a solution. The following is obtained from testing each candidates:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle 24\cdot \left(-1\right)^3-26\cdot \left(-1\right)^2+9\cdot \left(-1\right)-1 & = & \displaystyle -60 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 24\cdot 1^3-26\cdot 1^2+9\cdot 1-1 & = & \displaystyle 6 \ne 0 \\\\ x & = & \displaystyle -\frac{1}{2} &:&    & \displaystyle 24\left(\frac{-1}{2}\right)^3-26\left(\frac{-1}{2}\right)^2+9\left(-\frac{ 1}{ 2}\right)-1 & = & \displaystyle -15 \ne 0 \\\\ x & = & \displaystyle \frac{1}{2} &:&    & \displaystyle 24\left(\frac{1}{2}\right)^3-26\left(\frac{1}{2}\right)^2+9\cdot \frac{1}{2}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{3} &:&    & \displaystyle 24\left(\frac{-1}{3}\right)^3-26\left(\frac{-1}{3}\right)^2+9\left(-\frac{ 1}{ 3}\right)-1 & = & \displaystyle -\frac{70}{9} \ne 0 \\\\ x & = & \displaystyle \frac{1}{3} &:&    & \displaystyle 24\left(\frac{1}{3}\right)^3-26\left(\frac{1}{3}\right)^2+9\cdot \frac{1}{3}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{4} &:&    & \displaystyle 24\left(\frac{-1}{4}\right)^3-26\left(\frac{-1}{4}\right)^2+9\left(-\frac{ 1}{ 4}\right)-1 & = & \displaystyle -\frac{21}{4} \ne 0 \\\\ x & = & \displaystyle \frac{1}{4} &:&    & \displaystyle 24\left(\frac{1}{4}\right)^3-26\left(\frac{1}{4}\right)^2+9\cdot \frac{1}{4}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{6} &:&    & \displaystyle 24\left(\frac{-1}{6}\right)^3-26\left(\frac{-1}{6}\right)^2+9\left(-\frac{ 1}{ 6}\right)-1 & = & \displaystyle -\frac{10}{3} \ne 0 \\\\ x & = & \displaystyle \frac{1}{6} &:&    & \displaystyle 24\left(\frac{1}{6}\right)^3-26\left(\frac{1}{6}\right)^2+9\cdot \frac{1}{6}-1 & = & \displaystyle -\frac{1}{9} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{8} &:&    & \displaystyle 24\left(\frac{-1}{8}\right)^3-26\left(\frac{-1}{8}\right)^2+9\left(-\frac{ 1}{ 8}\right)-1 & = & \displaystyle -\frac{165}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{8} &:&    & \displaystyle 24\left(\frac{1}{8}\right)^3-26\left(\frac{1}{8}\right)^2+9\cdot \frac{1}{8}-1 & = & \displaystyle -\frac{15}{64} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{12} &:&    & \displaystyle 24\left(\frac{-1}{12}\right)^3-26\left(\frac{-1}{12}\right)^2+9\left(-\frac{ 1}{ 12}\right)-1 & = & \displaystyle -\frac{35}{18} \ne 0 \\\\ x & = & \displaystyle \frac{1}{12} &:&    & \displaystyle 24\left(\frac{1}{12}\right)^3-26\left(\frac{1}{12}\right)^2+9\cdot \frac{1}{12}-1 & = & \displaystyle -\frac{5}{12} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{24} &:&    & \displaystyle 24\left(\frac{-1}{24}\right)^3-26\left(\frac{-1}{24}\right)^2+9\left(-\frac{ 1}{ 24}\right)-1 & = & \displaystyle -\frac{91}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{24} &:&    & \displaystyle 24\left(\frac{1}{24}\right)^3-26\left(\frac{1}{24}\right)^2+9\cdot \frac{1}{24}-1 & = & \displaystyle -\frac{385}{576} \ne 0 \\\\ \end{array}\]

But since we have found all the required roots among the rational candidates, we find that \(\displaystyle x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \), so then:

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \]

which completes factorization process.

Result: Therefore, the final factorization is:

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right)\]

Therefore, the roots found are \(\frac{1}{2}\),\(\frac{1}{3}\) and \(\frac{1}{4}\) .

Other useful polynomial calculators

Finding zeros of a polynomial is one the pinnacles of Algebra, to the degree that the Fundamental Theorem of Algebra is about the existence of n roots for a polynomial of degree n. Those roots will not necessary be all real, and some of them (or all of them) may be complex numbers.

A very useful tool to gather properties about the number of positive and negative roots is Descartes Rule of Signs, which by simply counting sign changes between consecutive coefficients of the polynomial can tell you a lot about the types of roots of a polynomial (positive or negative)

Ultimately, almost every single problem in Algebra and Calculus can be reduced to finding roots of a polynomial, including solving polynomial equations, such as the ones you would find for example, when looking for the intersection between the graphs of \(y = x^2\) and \(y = x^3\).