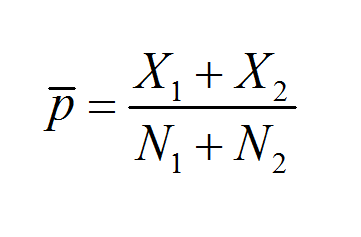Pooled Proportion Calculator

The idea of a pooled proportion is the following: Say we have sample information from the populations that have the same proportion. And then, you could use both samples individually to estimate such population proportion.

• If we use the information from the first sample, we would estimate the population proportion with \(\hat p_1 = \frac{X_1}{N_1}\).

• If we use the information from the second sample, we would estimate the population proportion with \(\hat p_2 = \frac{X_2}{N_2}\).

But if both samples come with populations with the same population proportion, why would we should one over the other?? That is when we would use the concept of pooled proportions, where we incorporate information from both samples to get one estimate of the population proportion.

What is the Formula of the Pooled proportion?

The pooled proportion is computed using the following formula:

\[\bar{p}=\frac{{{X}_{1}}+{{X}_{2}}}{{{N}_{1}}+{{N}_{2}}}\]

This way, with the above formula, we incorporate information from BOTH sample, by adding the number of favorable cases for the first and second sample, and dividing by the total number of cases, considering both samples.

Related Z-test

The pooled proportions is used in the z-test for two proportions , to construct an estimate a common population proportion under the assumption that the null hypothesis is true.