Domain and Range
The domain of a function is a set where a function is well defined. More specifically, let \(f: D \rightarrow R\) be a function, which means that \(f(a)\) is well defined for \(a \in D\). The domain of the function \(f\) is the set \(D\).
Mathematically you will write \(dom(f) = D\).
The range of a function, on the other hand, is a set of values that can be reached via the function.
More specifically, let \(f: D \rightarrow R\) be a function, the range is the set of all possible values \(b \in R\) for which there exists \(a \in D\) such that \(f(a) = b\).
Often, the range of a function is written as \(R(f)\) or also as \(f(D)\) (which is also known as the image set of \(D\) through the function \(f\)).
It is crucial to know the domain of a function because that gives us a safe set of values on which the function is well defined.
Then, the range is important because it tells us to what values are reached by the function. A more graphical interpretation is this: A point \(b\) is in the range of \(f\) if the horizontal line \(y = b\) intersects the graph of the function \(f(x)\).
How to compute the Domain, in practical terms?
Here is how to find domain and range :
For the domain, you need to find first the points where the function is NOT defined. The sources of undefined operations are division by zero or squared root of a negative numbers.
So, you need to find those points (if any) where those undefined operations occur. And the domain will be the rest of the points, this is, all the points excluding those you find that cause undefined operations.
How to compute the Range, in practical terms?
Let \(y\) be a number and we will solve for \(x\) the following equation \(f(x) = y\). The value \(y\) is in the range if \(f(x) = y\) can be solved for \(x\).
So this is a bit trickier: you need to find if you need to restrict \(y\) in any way so that \(f(x) = y\) has a solution for \(x\).
EXAMPLE 1
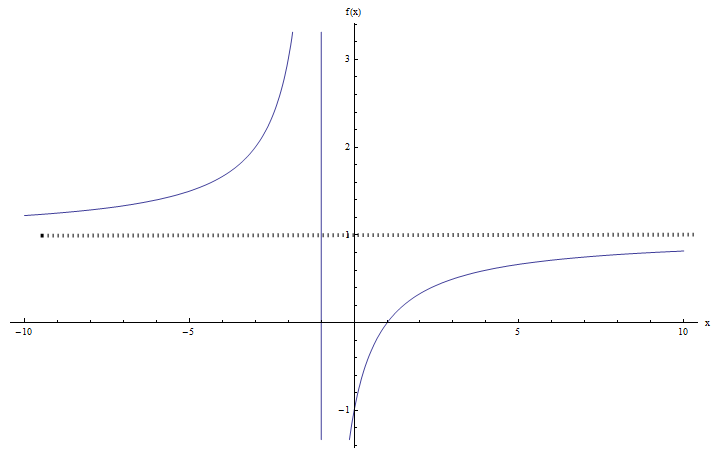
Calculate the domain and range of the function \(\displaystyle f(x) = \frac{x+1}{x-1}\).
ANSWER:
First, we need to compute the domain. We need to see where the function is well defined. Usually it is easier to start with where it is NOT well defined.
So in this case, all seem to be valid operations, except for one thing: the denominator cannot be zero.
Note: The main keys to find the domain is identify the points where there are potential divisions by zero, or potential square roots of negative values, which are invalid operations.
Therefore, the function is well defined EXCEPT when \(x-1 = 0\), which occurs when \(x = 1\). Hence, we say that the domain is the whole real line except for the value \(1\).
Using interval notation, we would write \(dom(f) = (-\infty, 1) \cup (1, +\infty)\).
Now we need to compute the range. Typically, it may be a bit more laborious to get the range than it is to get the domain, but here we go.
There are many ways to find the range: Some may rely on the graphical representation of the function to make a claim about the range of a function. That could work, but it is not a real answer, only a educated hunch.
The other way is the formal mathematical way: Let \(y\) be a number and we will solve for \(x\) the following equation \(f(x) = y\). The value \(y\) is in the range if \(f(x) = y\) can be solved for \(x\).
In this case we have:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-1} = y\] \[\Rightarrow \,\,\,x+1=y\left( x-1 \right)\] \[\Rightarrow \,\,\,x+1=yx-y\] \[\Rightarrow \,\,\,x-yx=-1-y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-y\] \[\Rightarrow \,\,\,x=\frac{y+1}{y-1}\]So, when is \(x\) well defined? Almost for all \(y\), except for when \(y = 1\), because in that case we have a division by \(0\). Hence, the range of \(f\) in this case is the whole real line, except for 1.
Using interval notation, we would write \(R(f) = (-\infty, 1) \cup (1, +\infty)\).
EXAMPLE 2
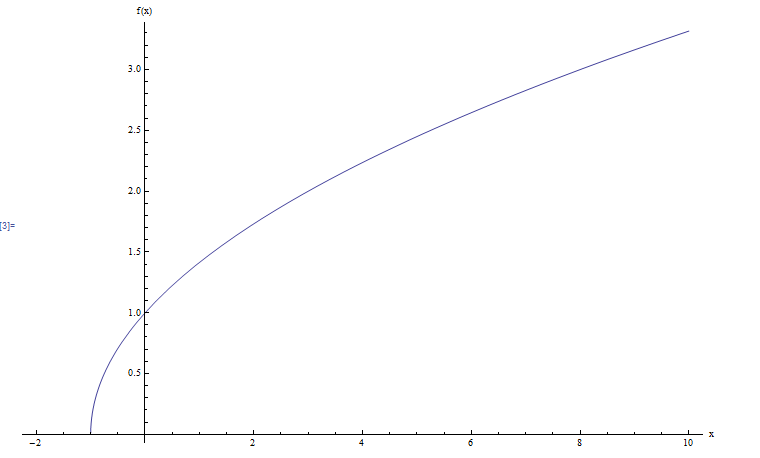
Calculate the domain and range of the function \(\displaystyle f(x) = \sqrt{x+1}\).
ANSWER:
Remember, for finding the domain we need to look for points where invalid operations may occur (divisions by zero or square roots of negative values. There are no divisions in this case, but we need to ensure that \(x+1\ge 0\) so that there are no square roots of negative values. So then we need \(x \ge -1\). Using interval notation, we would write \(dom(f) = [-1, +\infty)\).
.Now for the range, we need to solve for \(x\): \(\sqrt{x+1} = y\). The square root of something is never negative, so at least we need that \(y \ge 0\).
Also, by applying square to both sides, we get \(x+1 = y^2\), so then the solution is \(x = y^2-1\). So, the only restriction we need to impose on \(y\) is that \(y \ge 0\). Hence, using interval notation, we would write \(R(f) = [0, +\infty)\). Graphically:
More About the Domain and Range
As a way of a summary, let us recap a few things. First the domain is where a function is well defined, and the range is the set of points that are reached through the function.
In terms of the calculations required, it is typically easier to find the domain than finding the range. Normally, some people try to find the range graphically, but that is a potentially less precise way. Graphical answers need to be interpreted with caution.
You can check out tutorials specifically about how to find the domain and the range , which focus specifically on each case in more detail.
