More about the Graph of Inverse Functions

This calculator with help you to find the graph of the inverse function you provide, provided that the function has an inverse, which is not always the case.

You can provide a function in the format 'y = 2x - 1', or simply give an expression like 'f(x) = (x-1)/(x-3)' or just '(x-1)/(x-3)' to specify the function.

Once you have provide a valid function, you can click on the "Calculate" button, and you will be provided with all the steps of the calculation of the inverse function, and if the inverse exists, then a graph with the function and the inverse will be shown..

Observe that in order for the given function to have an inverse function, the function needs to be one-to-one, which means that every value in the range of the function has at most one pre-image in the domain of the function, and exactly one pre-image in we restrict effective range.

How to Know if a Function is Invertible

Before getting the graph of the inverse for a given function, you need to know whether the function has an inverse at all. The main criterion for having an inverse is being one-to-one, which means that one value in range cannot have two associated values (preimages).

Possibly students prefer not to use technical terms such as 'images' and 'preimages', and though those are core concepts in function theory, in this case we can use a simple graphical test to assess whether or not a function is one-to-one, and hence, if you can find and graph its inverse.

Horizontal Line Test

The horizontal line test indicates that in order for a function to be one-to-one, then any horizontal line you construct will cross the graph of the function at most once. If you are able to find one horizontal line that crosses the graph of the given function more than one time, then the function IS NOT one-to-one.

For example, the function shown below is one-to-one, because no matter what horizontal line we throw at it, it will cross the graph of the function exactly once:

But then, the next example shows a function that is not one-to-one, because we see a horizontal line that crosses the line of the function 2 times (more than once) :

Steps for finding the inverse graph

• Step 1: There are two common methods: one is the graphical method, and the other is the analytical method
• Step 2: For the graphical method, you need to first apply the horizontal line test and make sure it passes it, so it is one-to-one, and the inverse exists
• Step 3: Then, you draw the line y = x in the graph (a straight line that has a angle of 45^o degrees with respect to the x-axis
• Step 4: After that you simply use the line y = x as a 'mirror' and reflect the points of the original graph with respect to the 'mirror'. The obtained graph with this mirroring process is the graph of the inverse
• Step 5: For the analytical method, you need to first algebraically find the inverse: You start with y = f(x) and then solve for y.
• Step 6: If there is one solution only, then the inverse exist and you write it x = g(y). Adjusting the variable names, you define formally the inverse function \(f^{-1}\) in terms of g
• Step 7: Finally, you graph the inverse you found \(f^{-1}\) as you would graph a function normally

When you need to find the graph an inverse, both the graphical and analytical methods are fine, only the analytical method has an advantage, which is that you calculate the inverse function along the process, so you end up having a mathematical expression of it, not only its graph.

Why would you graph the inverse

There are so many why you would do that. First, the inverse function in itself is a very important actor in function theory, as a function shows how to pass from an x to a y, so it is only natural to want to know what the mechanism is to pass from y to x, and that is precisely what the inverse function provides you.

So, one could think of a function as a one-way map from a point "X" to a point "Y", and calculating the inverse function is like explicitly defining a map to go from "Y" to "X".

And then the graph of the inverse will tell you a lot of information about that inverse function: does it go down up, how it behaves.

How this inverse graph function calculator helps me?

First, this calculator will analyze the function to see if it is invertible by using the analytic method, and if it is possible to find such inverse, it will graph it for you.

Finding the inverse involves solving an equation, which is not an easy task unless you are dealing with linear equations or polynomial equations, but other than that, the process can be very complex or even impossible.

Other calculators may do a similar process, but one of the advantage of this calculator is that it provides all the the steps of the process, with a detailed explanation, where possible.

Example: Finding the graph of the inverse

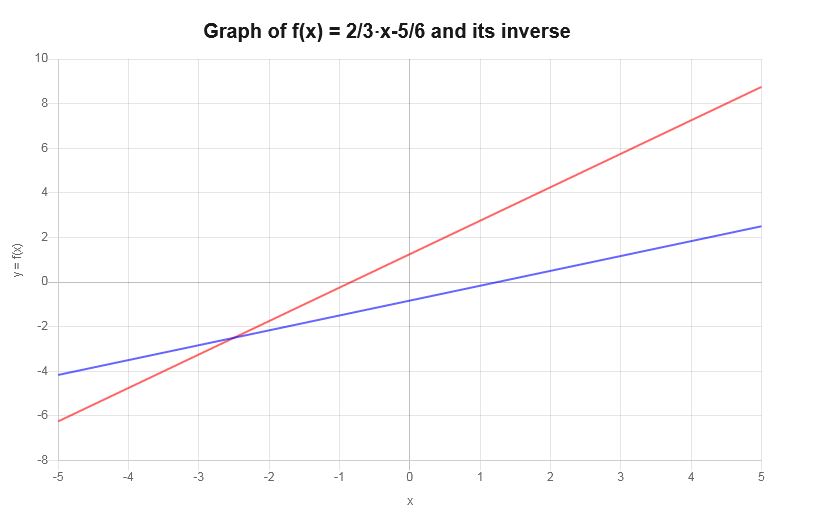
Graph the inverse of : \( y = \frac{2}{3} x - \frac{5}{6}\)

Solution:

We have been provided with the following function:

\[ y = \frac{2}{3} x - \frac{5}{6}\]

Then, in order to find the inverse of the given function, we need to solve for \(x\) and determine whether there is a solution or not. The starting equation is

\[y=\frac{2}{3}x-\frac{5}{6}\]

Step 0: In this case, we first need to simplify the given linear equation, and in order to do so, we conduct the following simplification steps:

Solving the Linear Equation

Putting \(x\) on the left hand side and \(y\) and the constant on the right hand side we get

\[\displaystyle -\frac{2}{3}x = -y -\frac{5}{6}\]

Now, solving for \(x\), by dividing both sides of the equation by \(-\frac{2}{3}\), the following is obtained

\[\displaystyle x=-\frac{1}{-\frac{2}{3}}y-\frac{\frac{5}{6}}{-\frac{2}{3}}\]

and simplifying we finally get the following

\[\displaystyle x=\frac{3}{2}y+\frac{5}{4}\]

Therefore, the solving for \(y\) for given linear equation leads to \(x = \frac{3}{2}y+\frac{5}{4}\).

Therefore, and since when solving for \(x\) we find a solution and it is only one solution, we have found the inverse.

The Inverse Function Found

Based on the work shown above, it can be concluded that the inverse function is:

\[f^{-1}(x) = \frac{3}{2}x+\frac{5}{4}\]

The inverse function can be shown graphically as follows:

Example: More inverse graphs

Can you find the inverse graph of: \(y = x^2\)

Solution: No, we cannot find the inverse graph of \(y = x^2\), as this function does not pass the horizontal line test. Another way to see it is that when solving for \(x\) we get \(x = \pm \sqrt y\), and since we find two solutions, then there is no inverse, and consequently, there is no inverse graph.

More function calculators

Functions and any type of function operations are truly the center of Algebra and Calculus. A good function calculator will make your life easier in terms of reducing a function to its simplest expression.

Then, you will have a good function graphing tool in order to take a quick glimpse at the graphical properties of a function. Seeing the graph of a function can tell you a lot about its behavior, even before looking at its algebraic expression.

Then you have more advanced operations such as finding the derivative, for which this differentiation calculator will come in handy, as it shows you all the steps of the process. As expected, the derivative of the inverse function has an interesting association with the derivative of the original function.