Calculating the area of circles from diameter

This calculator will allow you compute the area of circles, provided that you provide the diameter. The diameter provided needs to be any valid positive expression. It could be a number like '2', it could be a fraction like '3/4' or it could a expression involving square roots, like '3sqrt(3)'.

Once a valid diameter is provided, the area of the circle will be calculated showing all the steps once you click on the "Calculate" button.

Normally, you would compute the area of the circle based on the radius, but it is not uncommon to want to go directly from diameter to area, and this calculator does exactly that.

How to compute the area of circle from diameter?

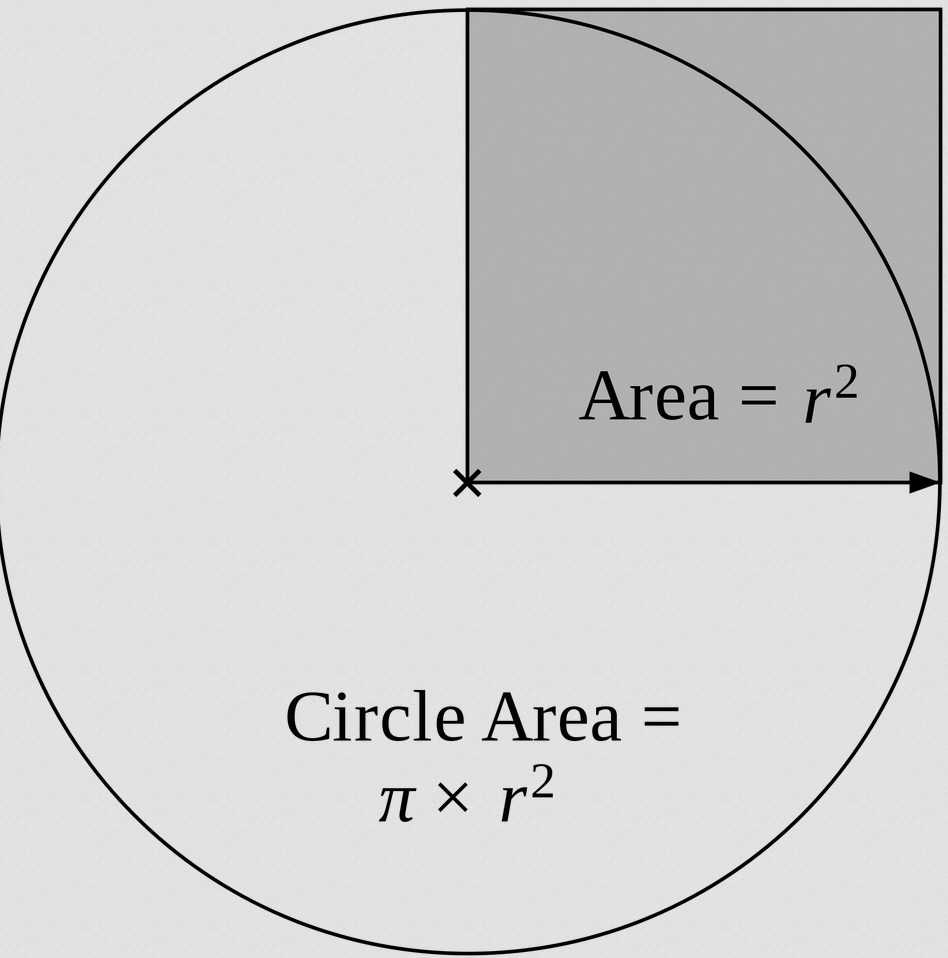
We all know the famous area of circle formula:

\[ A = \pi r^2 \]

The only "problem" is that this circle formula requires the radius. But notoriously, the radius (r) and diameter (d) are related through the formula \(r = \frac{d}{2}\)

Then, plugging this into the above area formula, we get

\[ A = \pi r^2 = \displaystyle \pi \left(\frac{d}{2}\right)^2 = \displaystyle \pi \cdot \frac{d^2}{4} \]

which gives us a direct formula to go to the area from the diameter.

What are the steps for getting from diameter to area?

• Step 1: Identify clearly the diameter given. Make sure it is positive, otherwise you cannot proceed
• Step 2: Once you have a valid diameter, you plug d it into the formula \(A = \displaystyle \pi \cdot \frac{d^2}{4}\)
• Step 3: If the diameter d has units, the area will have those same units, but squared

For example, if the diameter is measured in cm, then the area is measured in cm².

Now, you may be interested in the reverse problem, where you want to compute the diameter of a circle from its area.

The Radius and diameter

Interestingly enough, the radius and diameter are broadly used, though it could seem that the radius is sort of more popular. Geometrically speaking, it is the diameter that is perhaps the natural choice for the default circle formulas, but that is not the case.

You always have the choice of going from the given diameter to the radius, by simply dividing the diameter by 2, and work all the default formulas that use the radius instead.

Why would you use the diameter instead of the radius?

Different reasons, perhaps conceptually is not really relevant. But yet, when considering the the diameter of a circle formula, we would see that \(C = \pi d\), or in other words, the ratio between circumference and diameter for any circle is constant, and that constant is called \(\pi\).

A similar statement can be made involving the radius, but it looks a lot more concise this way.

Example: Calculating area from the diameter

Assume that the diameter of a circle is d = 12, find the area.

Solution: We are given the diameter d = 12, and we have the following area formula for a given diameter:

\[ A = \displaystyle \pi \cdot \frac{d^2}{4} = \displaystyle \pi \cdot \frac{12^2}{4} = \displaystyle \pi \cdot \frac{144}{4} = 36 \pi\]

which concludes the calculation.

Example: Diameter, radius and area?

Given a diameter of d = 2, use the common area formula that uses the radius.

Solution: From a diameter of d = 2, we know that by dividing the diameter by 2 we get the radius, so in this case, r = 2/2 = 1.

Using the traditional area formula, \(A = \pi r^2 = \pi \cdot 1^2 = \pi\), we find that that area is \(\pi\).

which concludes the calculation.

Example: Can you compute the area?

For a given diameter of d = -4, can you compute the area?

Solution: This is a great example of where the "can you" may be true, when the "should you" is not. Indeed, from the formula derived above for the area from the diameter, we get

\[ A = \displaystyle \pi \cdot \frac{d^2}{4} \]

Naively, you could "plug-in" the value d = -4 in the above formula, to get:

\[ A = \displaystyle \pi \cdot \frac{d^2}{4} = \displaystyle \pi \cdot \frac{(-4)^2}{4} = \displaystyle \pi \cdot \frac{(16}{4} = 4\pi \]

which means that you actually "can" compute the area for a negative diameter. The question is "should you"? The answer is NO, because it does not have geometric meaning to have a circle with a negative diameter (for now).

Other useful circle calculators

Circles are literally among the most important objects in mathematics. From computing the area of the circle, to computing its circumference, we have different formulas that help us with those tasks.

The idea of areas and circumferences is mostly geometric ones, as we don't need to know the equation of the circle to compute them.