The Parabola
A parabola is the geometric place of points in the coordinate axes that have the property that they are equidistant from a fixed point (called the focus) and a line (called the directrix).
I know what sounds a bit too technical, but we will go through it, and in the end you will see it is not that hard.
So, would it help if I told that that
the function \(f(x) = x^2\) represents a parabola?
Sure it will help. And you may be thinking "why you did not tell me from the beginning that the parabola is that function?".
Because there is not A parabola, there is a infinite number of them. And a parabola does not even have to be represented by a function. Yes, some relations are parabolas, as we will see.
One thing is important to be mentioned: Using functions and relations, there are the parabolas that "open up" along the \(y\)-axis, and there are the parabolas that "open up"along the \(x\)-axis.
In the end, by symmetry, it is easy to realize that those parabolas that "open up" along the y-axis have the same structure as those that "open up" along the x-axis, so it is enough to learn how to handle one type.
The General Equation of the Parabola
There are simple derivations to get the equation of a parabola based on the location of a directrix and the focus, but we will skip the derivation in this introduction.
Check the graph below. We need to identify some crucial elements of the parabola: We have the vertex, the focus and the directrix.
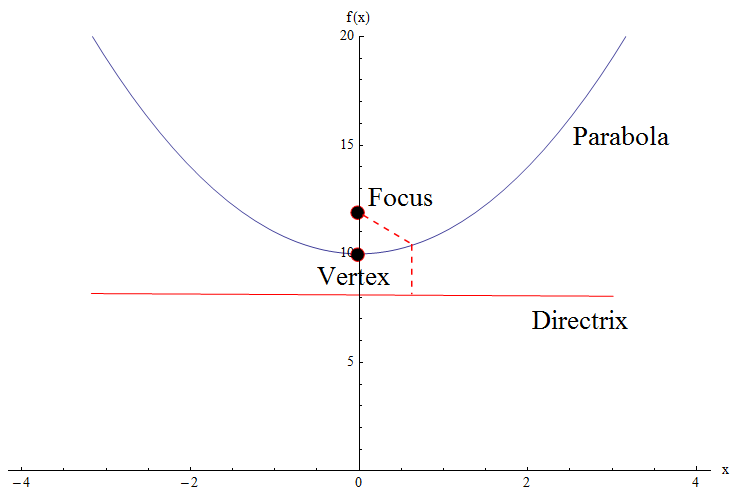
We won't into much detail, but we will say the equation of a general parabola with vertex at the origin, with focus \((0, a)\) and directrix equal to \(y = -a\) is
This parabola is the kind of parabola that opens up along the y-axis.
Now what happens when instead of having the vertex at the origin, we want to have the vertex at a given point \((k,h)\)?
Well, that is the magic of working with a coordinate system, and all we need to do a translation by the point point \((k,h)\)? But how do you do a translation by \((k,h)\)?
Simple! Wherever you have \(x\), you replace it by \(x-k\), and wherever you have \(y\), you replace it by \(x-h\).
Hence, doing a translation, the equation of a general parabola with vertex at the point \((k,h)\), with focus \((k, h+a)\) and directrix equal to \(y = h-a\) is
\[\large y-h = 4a(x-k)^2\]which can be written as
\[\large \boxed{ y = 4a(x-k)^2 + h }\]What happens with the parabolas that open up along the x-axis?
By symmetry, this simply obtained by replacing the roles of \(x\) and \(y\) in the equation of the parabola we already have. In practicality, this means that wherever \(x\) appears in the equation of the parabola we have, we change it \(y\), and vice versa for \(y\).
Therefore, the equation of a general parabola with vertex at the point \((h,k)\), with focus \((h+a, k)\) and directrix equal to \(x = h-a\) is:
\[\large \boxed{ x = 4a(y-k)^2 + h }\]Notice the difference:
When a parabola has a directrix of the form \(y = -a\), then the parabola opens along the y-axis (up or down depending on whether the focus is above or below the directrix).
When a parabola has a directrix of the form \(x = -a\), then the parabola opens along the x-axis (left or right depending on whether the focus is to the left or right of the directrix).
EXAMPLE 1
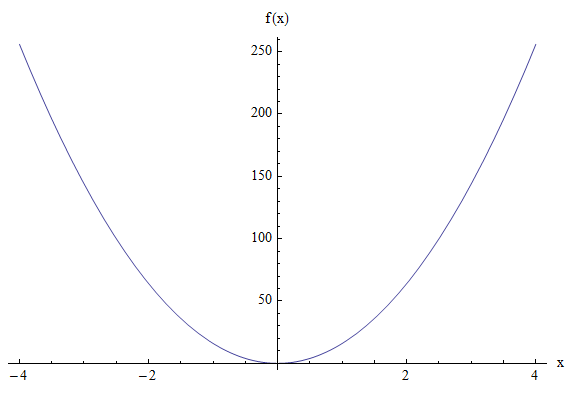
Find the equation of the parabola that has a directrix \(y = -4\) and a focus \((0, 4)\). Also find the vertex.
ANSWER:
The vertex is the on the parabola, so it is equidistant from the directrix \(y = -4\) and the focus \((0, 4)\), so then the vertex is \(0, 0)\). On the other hand, for a parabola with vertex at the origin, the equation of the directrix is \(y = -a\), so then in this case \(a = 4\). Consequently, the equation of the parabola is
\[ \large y = 4ax^2 = 4(4)x^2 = 16x^2 \]Graphically:
EXAMPLE 2
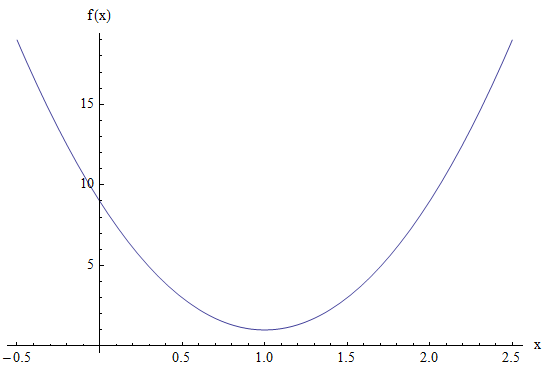
Find the vertex, focus and directrix of the parabola \(y = 8x^2 - 16x + 9\).
ANSWER:
First of all, we need to complete the square:
\[\large y = 8x^2 - 16x + 9 = 8(x^2 - 2x) + 9 \] \[\large = 8(x^2 - 2x + 1 - 1) + 9 \] \[\large = 8(x^2 - 2x + 1) + 9 - 8 \] \[\large = 8(x-1)^2 + 1 \]Equating this with the general equation, we find that the vertex is at the point \((1, 1)\), and also we have that \(4a = 8\), so \(a = 2\), hence, the directrix is \(y = h - a = 1 - 2 = -1\) and the focus is \((k, h + a) = (1, 1+2) = (1, 3)\).
Graphically:
The Parabola and general Conic Sections
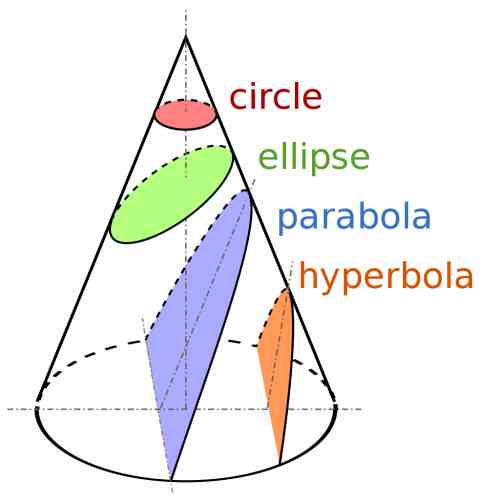
As strange as it may be, the parabola is tightly related to the cone. How, would you say? A Greek mathematicians named Apollonius is credit with having contributed with the modern version, using coordinate systems, of the conic sections.
Apollonius and other mathematicians discovered that when you cut a cone with a plane, depending on the relative angle of the cone and the plane, the cone is cut in a way that the section has different shapes.
The different shapes of the sections, depending of the relative angle of cut are what we know as the parabola, circle, ellipse, and hyperbola, as show in the figure below:
More About the Parabola
A general parabola that opens along the y-axis, with vertex at the origin \((0, 0)\) has the following functional representation \(y = 4ax^2\).
Then, by symmetry, a general parabola that opens along the x-axis, with vertex at the origin \((0, 0)\) has the following functional representation \(x = 4ay^2\).
Then, a general vertex can be obtained by applying a translation to a given point \((k, h)\).
Applications
The parabola has countless applications in Physics, because of the way the gravity force and Newton's laws operate, the trajectory of most bodies that are thrown out will follow a parabolic trajectory.
Also, algebraically speaking, parabolas appear in Algebra all the time, because all quadratic functions have a parabolic graph, and quadratic functions appear a LOT in Algebra.
Also, parabolas appear in Calculus when finding minima and maxima. It turns out that many maximization and minimization problems have a quadratic function to maximize, and geometrically, the maximum or minimum (depending on if the parabola opens up or down) is achieved at the vertex.
Other conic sections you may be interested in learning about are the ellipse , the hyperbola and the circle .