The Equation of the Circle
A circle is one of the most notable geometric figures. It has some remarkable symmetry, based on the fact that ALL points in the circle are equidistant from the center, which in English means that all the points in the circle are the same distance from the center. This common distance \(r\) is called the radius of the circle .
The circle has some many important geometric applications, which make it make a really important object in both geometry and algebra.
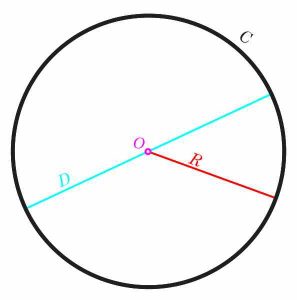
Another crucial property of the circle is that it is very easily represented algebraically. This means that we can easily set an equation to represent all the points in a given circle. To put it more concretely, consider the coordinates plane \(X - Y\). All this means is that we have the X and Y axes, which are perpendicular to each other
Equation of the Circle
Now, let us talk about the equation that represents all the points of a given circle. Indeed, for a circle of radius \(r\), the following equation describes points \((x, y)\) that are on the circle:
\[\Large x^2 + y^2 = r^2\]The above corresponds to the equation of a circle of radius \(r\), with at center located at \((0,0)\), the origin of the coordinate axes.
When the radius is \(r = 1\), then we have what is called a unit circle.
When looking at the equation above, the geometric interpretation is that \(x\) and \(y\) are the sides of a triangle and \(r\) is its hypotenuse
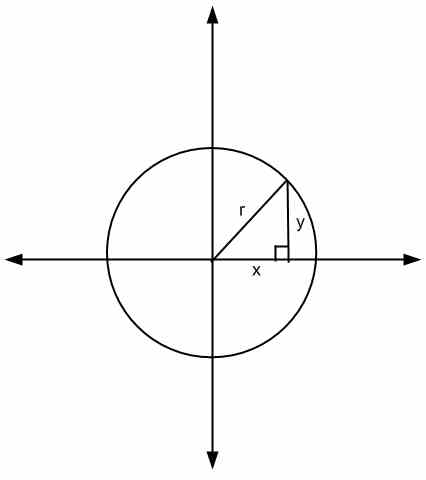
Another way of seeing the equation of the circle is by taking square root to both sides of the equation, so we would get \(\sqrt{x^2+y^2} = r\), which indicates that for any point \((x,y)\) on the circle, the distance to the origin (in this case, the center of the circle) is equal to \(r\).
Equation of a Circle that is Not Centered at the Origin
One advantage of working on coordinated axes is that the points on the circle, and the center, can be localized in the axes, and can be represented by an equation, as shown above. But in general, the center of the circle does not have to be the origin, it can be any point \((x_0, y_0\) in the coordinated axes, in which case, the equation of the circle becomes:
\[\Large (x-x_0)^2 + (y-y_0)^2 = r^2\]which is known as the General Equation of a Circle . For example, say you need to compute the equation of a circle of radius \(r = 4\), that is centered at the point \((1,2)\). So in this case, we have \(x_0 = 1\), \(y_0 = 2\) and \(r = 4\), and then we just plug these numbers into the above equation and we get
\[\large (x-1)^2 + (y-2)^2 = 4^2\]or we can also write
\[\large (x-1)^2 + (y-2)^2 = 16\]EXAMPLE 1
Write the equation of the circle of radius 3, with center at the origin. Using the equation, determine whether or not the point (1, 2) belongs to the circle.
ANSWER:
First, let us determine the equation of the circle. In this case, the circle is centered at the origin, so then \((x_0, y_0) = (0, 0)\). Hence, the equation is
\[\large x^2 + y^2 = 3^2\]which is the same as
\[\large x^2 + y^2 = 9\]Now, the question is whether or not the point (1, 2) is on the circle. We know that the points on the circle will such that \(x^2 + y^2 = 9\).
For the point \((1, 2)\) we get that \(x = 1\) and \(y=2\), so then for this case of that point, \(x^2 + y^2 = 1^2 + 2^2 = 1+ 4 = 5\) which is different from 9, and therefore \((1,2)\) does not belong to the circle.
More About the Equation of the Circle
The circle is such an important math entity, that volumes of books have been written about it. Circles cross Geometry, Trigonometry and Algebra, so that is why it is such as transversal appearance everywhere in Math.
How to Work out the Equation of a Circle?
When we work with a circle, there are several things to work out. The first thing is to construct the equation of the circle. For example, consider a circle of radius \(r = 3\), that is centered at the point \((1,1)\).
Based on the general equation of a circle, the equation is
\[\large (x-1)^2 + (y-1)^2 = 3^2\]The above equation can be used, for example, to determine whether a point belongs to the circle or not. What else can you do to work out the equation of the circle? You could potentially expand the squares, so we get
\[\large x^2 - 2x + 1 + y^2 -2y + 1 = 9\]which can be simplified into
\[\large x^2 - 2x + y^2 -2y = 7\]So, both equations are equivalent, in the sense that they determine the same circle. Which one do you prefer? \((x-1)^2 + (y-1)^2 = 3^2\) or \(x^2 - 2x + y^2 -2y = 7\)? It is matter of taste and what would you be using the formula for.
Area of a circle
Interestingly, in order to compute the area of a circle, you don't need the full equation of the circle, you just need to know the radius. In other words, the area and circumference of a circle do not depend on its center.
Is the equation of a circle a function?
This is a question many students have, and we need to clarify. First of all, the equation of the circle is an equation, not a relation or a function.
Now, the equation of the circle determines a relation, and not a function, when you algebraically solve for y in terms of x. Indeed, if we solve for \(y\) we get:
\[\large x^2 + y^2 = 9 \Rightarrow y^2 = 9 - x^2 \] \[\large \Rightarrow y = \pm \sqrt{ 9 - x^2} \]That means that for a given \(x\), there are two values of \(y\) that are associated, which are \(\sqrt{ 9 - x^2}\) and \(-\sqrt{ 9 - x^2}\), which indicates that the equation of the circle determines a relation instead of a function.
One specific case of the circle is the unit circle , with equation \(x^2 + y^2 = 1\), that is centered at the origin. The unit circle is especially suitable to work with trigonometric expressions in a very visual way.
