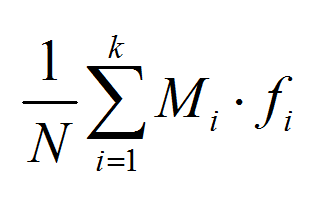Sample Mean of Grouped Data Calculator
Instructions: Use this Sample Mean of Grouped Data Calculator to find the sample mean when you have grouped data, in the form of classes and associated frequencies. Please type those classes and frequencies in the form below:
More about this Sample Mean of Grouped Calculator
It is not uncommon to have grouped data, as opposed to having raw data. When we say raw data, we mean individual data. So then, having raw data means having all the information of the sample.
But there are cases in which raw, individual data is not known, and we have grouped data. This is, we may have information like "the sample has 4 values on the class 3 - 5", which means that we know that the sample has 4 values between the values of 3 - 5, but we don't exactly where exactly those 4 values are. We only know a range.
What happens in that case is that we use the midpoint of the class to approximate (our best guess) for the values on that class.
Formula for the Sample Mean of Grouped Data
In order to compute the sample mean for grouped data, we have compute the corresponding midpoints of each class. Then, we have to use the following formula:
\[\text{Sample Mean of Grouped Data} = \frac{1}{N}\sum\limits_{i=1}^{k}{{{M}_{i}}\cdot {{f}_{i}}}\]where \(M_i\) corresponds to the midpoint of the i-th class, and \(f_i\) corresponds to the frequency of the i-th class.
Other Descriptive Statistics Calculators
If you are not looking for a measure of central tendency and instead you want a measure of dispersion for grouped data, you can use this sample variance calculator for grouped data .
For a more complete analysis of descriptive statistics of grouped data use this calculator . Also, you may be interested in using this percentile calculator for grouped data , which uses the interpolation formula.