More about this composite and prime number calculator

This calculator allows you to assess whether a given number is composite or prime, based on its factors. The provided number needs to be a valid positive integer . For example, you can provide a number like '3', '9', etc.

Once the valid positive integer is provided, then you need to click "Calculate", and the answer and steps will be provided.

The process is based upon finding the factors of the given number in order to make an statement of whether the number is composite or prime.

Is a number composite or prime?

A composite number is such that it has factors other than 1 and itself. On the other hand, a prime number ONLY has 1 and itself as factors. For example, 4 is not prime (so it is composite) since \(4 = 2 \cdot 2\), which means the 2 is a factor, and 2 is not 1 nor 4. On the other hand, 5 is a prime number, because its only factors are 1 and 5.

What are the steps for assessing whether a number is composite or prime

• Step 1: Identify the number you want to analyze. Continue the process only if it is a positive integer. Call the number 'n'
• Step 2: Find the factors of 'n'
• Step 3: If there is a factor that is neither 1 nor 'n', then the number is composite
\
• Step 4: If the only factors are 1 and 'n', then the number is prime

Why would you care about composite and prime numbers?

Often times, you would like to reduce fractions or simplify algebraic expressions, in which case it is useful to be able to see if numbers are composite or not, in order to attempt the simplification.

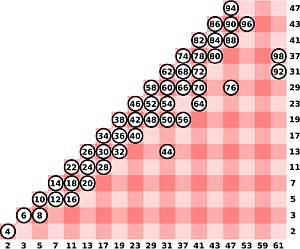
Example: Factors of a number

Calculate factors of 23. Is 23 prime or composite?

Solution: By checking all the possible prime divisors of \(n = 23\), we find that there are no factors other than 1 and 23, hence the number \(n = 23\) is prime, and the prime decomposition of \(n = 23\) is itself.

Example: Composite numbers

Is n = 10 composite or prime?

Solution: First, we need to assess whether \(n = 10\) has any prime divisors. In this case, it is found that

Since \(n = 10\) has at least one factor that is neither 1 nor itself, it is concluded that \(n = 10\) is composite.

Example: Composite versus prime

Is n = 47 prime or composite? How do you know?

Solution: By checking all the possible prime divisors of \(n = 47\), we find that it has no factor other than 1 and \(47\), and hence the number \(n = 47\) is prime, and the prime decomposition of \(n = 47\) is itself.

More algebra calculators

Calculating the prime decomposition of a number is a crucial property that numbers have, and it has many applications, including the one used by this calculator in the process of assessment of whether a number is composite or prime.

Indeed, knowing whether a number is composite or prime can help with the calculation of the greatest common divisor (GCD) as well as the least common multiple (LCM).