More about this determinant calculator.

In linear algebra and in the use of matrices, the idea of the determinant of a matrix \(A\) is a concept of the deepest importance.

This is because its use is tied with almost every significant operation you will want to do with matrices, such as verifying invertibility of matrices, finding the inverse of a matrix or solving systems.

So, wherever you look around when working with matrices, you will find determinants one way or the other. So, it is very important to become familiar with them.

How can this matrix calculator help you

1. All you need to do is to type your matrix
2. It needs to be a square matrix, this is, a matrix with the same number of rows and columns
3. Just click the button and the calculator will show you all the steps and the final value of the determinant
4. Working on determinant calculations can be extremely laborious and prone error. This calculator spare you from those problems

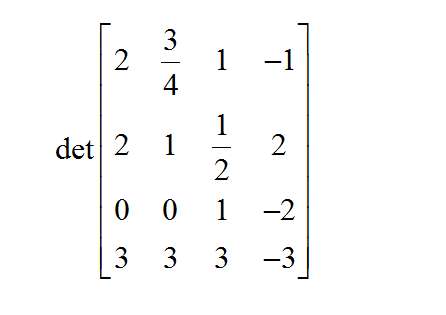
How do you compute the determinant of a matrix?

That could be a long answer, because there are many ways to compute the determinant of a matrix. Let us saying first that determinant are only computing for square matrices (this is matrices that have the same number of rows and columns).

So, the smallest matrix we can compute a determinant for is a 2x2 matrix. Let us consider a generic 2x2 matrix, as shown below:

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

What is the formula of the determinant? In this case, the determinant of the matrix \(A\) is simply computed as \(\det(A) = a d - bc\)

So for example, if we had:

\[ A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\]

the determinant of the matrix \(A\) would be \(\det(A) = 1 \cdot 3 - 2 \cdot 1 = 3 - 2 = 1\). Easy, right?

How do you find the determinant of a 3x3 matrix?

Now, for larger matrices, we build the calculation of the determinant based on sub-determinant of smaller matrices. Just to give you a flavor, let's see one way of computing the determinant of a 3x3 matrix. Consider

\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]

In this case, the determinant of the matrix 3x3 matrix \(A\) is computed based on the operation of several 2x2 determinants

\[\det(A) = a \det \begin{bmatrix}e & f \\ h & i \end{bmatrix} - b \det \begin{bmatrix} d & f \\ g & i \end{bmatrix} + c \det\begin{bmatrix} d & e \\ g & h \end{bmatrix}\]

In the above equations the values \(a\), \(b\), \(c\) play the role of pivots, and the may get a negative sign. The sign of a pivot is \((-1)^{i+j}\), where the corresponding pivot is in row \(i\) and column \(j\).

For example \(a\) is in row 1, column 1, so its sign is \((-1)^{1+1} = (-1)^2 = 1\) (positive). Also, \(b\) is in row 1, column 2, so its sign is \((-1)^{1+2} = (-1)^3 = -1\) (negative), and so on.

The magic is to choose any row or column as pivots. Each pivot will have a sign associated (positive or negative) and a sub-determinant, which are related with the matrix cofactors.

This sub-determinant is the actual determinant of the original matrix after removing row \(i\) and column \(j\), for pivot that is in row \(i\) and column \(j\).

The most logical convention indicates to choose the row or colum with the most zeros for the pivots, so to avoid computing some of the sub-determinants, if possible.

How do you find the determinant of a 3x4 matrix?

You cannot do it. A 3x4 matrix is not a square matrix, and hence, no determinant can be computed. In order to compute a determinant, the matrix needs to have the same number of rows and columns.

A 4x4 determinant calculator

For larger matrices, the methodology is the same: Choose one row or column for pivots, ideally that with the most zeroes. The find the sign corresponding to each pivot, and find the corresponding sub-determinants.

So then, you reduce the calculation of the determinant of a 4x4 matrix into the operation of four 3x3 determinants. And in turn, each of 3x3 determinants are found as the operation of several 2x2 determinants, for which we know a formula.

So, it can get messy real quick.

Example of the calculation of a matrix determinant

Question: Consider the following matrix:

\[ \begin{bmatrix}1&2&3\\3&1&4\\2&3&8\end{bmatrix}\]

Compute the determinant of the given matrix, showing the steps.

Solution: We need to compute the determinant of the \(3 \times 3\) matrix that has been provided.

Using the sub-determinant formula we get:

\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 3&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 8 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 8 \right) - 3 \cdot \left(4 \right) \right) - 2 \cdot \left( 3 \cdot \left( 8 \right) - 2 \cdot \left(4 \right) \right) + 3 \cdot \left( 3 \cdot \left( 3 \right) - 2 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -4 \right) - 2 \cdot \left( 16 \right) + 3 \cdot \left( 7 \right) = -15\]

Conclusion: Based on the calculations shown above, it is found that the determinant of the matrix is \(\det A = \displaystyle -15\).

Other useful matrix calculators that you can use

Matrix calculations done by hand are labor-intensive, so you can take advantage of our linear algebra solvers.

First, you can use this inverse matrix calculator to compute the inverse of a matrix showing steps, and you can do it either by adjoint method, or by using RREF reduction.