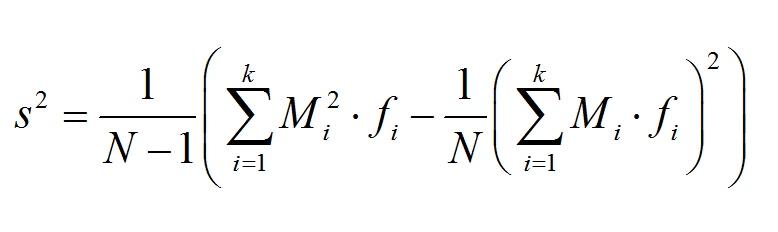More about this Sample Variance of Grouped Data Calculator

Having grouped data is a common situation, in which not all information is known about the sample. This is, we don't really know all the scores, one by one. We only know that within a certain range (a class), there are a certain number of values.

For example, we may know that the sample has 5 values between 4.5 and 6.5, although we don't know exactly where between 4.5 and 6.5 those values are. In the context that example, the class is 4.5 - 6.5, and the associated frequency is 5.

There is one way to deal with grouped data. This way consists of dealing with the midpoint of a class as the representative of those values in the class. Since we don't know exactly where in the class those values are, we choose to represent them by the midpoint. Mathematically, the midpoint of the i-th class is called \(M_i\).

Formula for the Sample Variance of Grouped Data

By using the midpoints are the representative of the values in the classes, we can use this familiar formula to get the variance of grouped data:

\[ s^2 = \frac{ 1}{N-1}\left(\sum_{i=1}^n M_i^2 \cdot f_i - \frac{1}{N}\left(\sum_{i=1}^n M_i \cdot f_i \right)^2 \right) \]

where the values \(M_i\) are the midpoints, \(n\) is the total number of classes, and \(N\) is the total sample size.

You may also want to look a these Descriptive Statistics Calculators

You can also use this sample mean of grouped data calculator if you are instead interested in computing the sample mean, because you may be interested in analyzing the measures of central tendency as opposed to the measures of dispersion

In case you want to dig deeper into the calculator of more descriptive statistics, check out this this calculator . A related calculator to use is percentile calculator for grouped data , aimed at providing a step-by-step calculation of percentiles using the method of interpolation, which differs slightly from the method used by Excel, for example.