Exponential Decay Calculator
Instructions: Use this step-by-step Exponential Decay Calculator, to find the function that describe the exponential decay for the given parameters. You need to provide the initial value \(A_0\), and the half life \(h\) OR one value of the function at a future time.
More about this Exponential Decay Calculator
A function \(f(t)\) has exponential decay if it can be expressed as:
\[f(t) = A_0 e^{-kt}\]The decay rate \(k\) can be either provided, or you may need to calculate it. The initial value \(A_0\) is typically provided.
There are basically two ways of giving information that you can use to compute \(k\). For both ways you will need the initial value \(A_0\). But that is not enough, and you will need one extra piece of information.
You can be either be provided with the corresponding half-life , OR you can be provided the value of the function at a certain future time.
For a more in depth analysis of exponential decay and its formula and properties, see this tutorial . Also you can use this exponential growth calculator for the case of exponential growth.
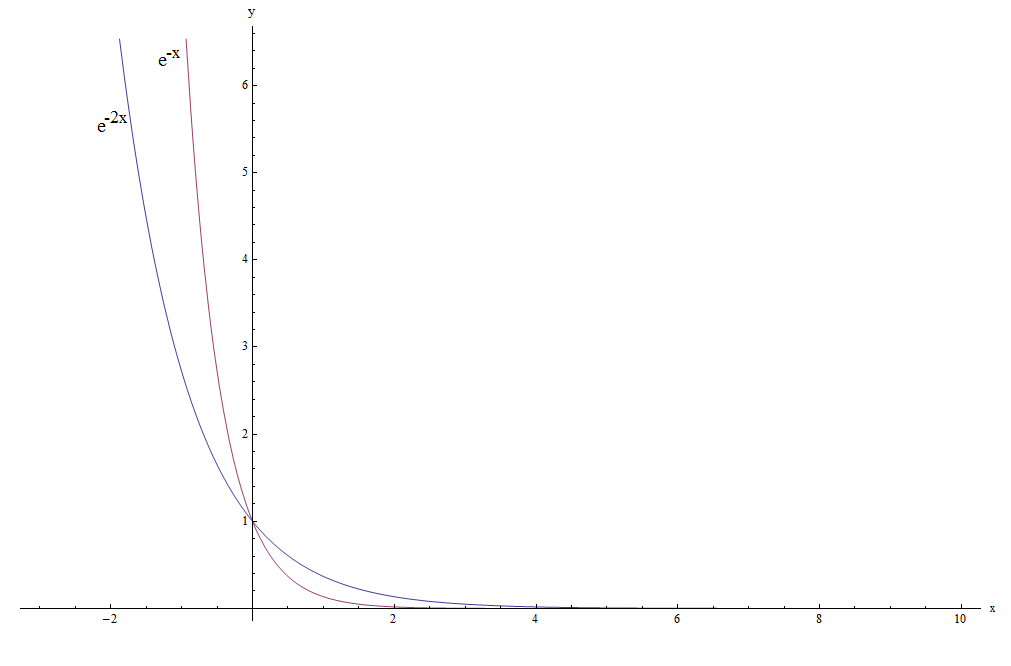
Also, it can be useful for you to graph