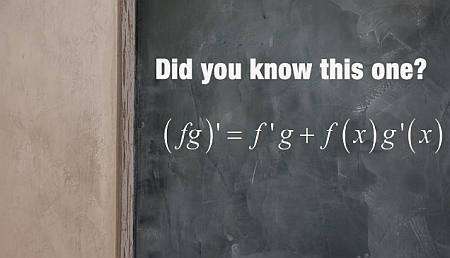More on the Product Rule
This calculator will help you finding the derivative of functions using the Product Rule. In order to use the calculator,
you need to provide a valid function for which there is a product involved.
An example of a valid function could something like f(x) = x*sin(x), or something like g(x) = sin(x)*cos(x), just to
mention a few.
Then, we are dong typing the function for which you want to use the product rule, you then have to click on, all you need to do is to click on the "Calculate" button,
and all the steps of the calculations will be provided to you.
One of the first rule of derivative that you will learn is indeed the Product Rule, as most of the functions you construct from elementary functions use
the product of functions.

Product Rule formula
Learning about derivative rule is perhaps the first you will do when learning on how to
find the derivative of a function. And one the first rules you will learn is the product rule, without a doubt.
The product rule, put simply, is a rule that helps you compute the derivative of a product of functions. The product rule formula is:
\[\displaystyle (f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \]
Steps for using the product rule
- Step 1: Identify clearly the functions f(x) and g(x) that form the product you are working with
- Step 2: Make simplifications if needed, while keeping the product structure
- Step 3: Use the product rule formula: \((f(x) g(x))' = f'(x) g(x) + f(x) g'(x) \) which involves plugging the value of the functions f(x) and g(x), as well as
of its derivatives f'(x) and g'(x)
By working with a product rule derivative, you essentially are getting the derivative of the product based on the knowledge of the individual functions and
their derivatives.
What other derivative rules are there?
Aside from the product rule, there are other important rules such as the linearity rule, the quotient rule which states
that \(\frac{d}{dx} \left(\frac{f(x)}{g(x)}\right) = \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)}\), and
the chain rule, which states that \(\frac{d}{dx} f(g(x)) = f'(g(x))g'(x)\).
You will also find other rules mentioned around, such as as the power rule, which indicates that \(\frac{d}{dx} x^n = n x^{n-1}\), for a constant \(n\).

Tips and Tricks
The product rule can be considered as a derivative multiplication rule, and the product rule plays a crucial role in Calculus, so it pays off to learn it well.
Notice that in the case of multivariable functions, you can use the rule of matrix multiplication, in order to operate the product rule.
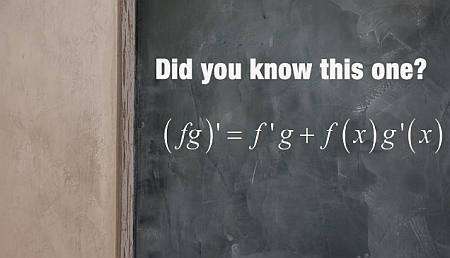
Example: Using the Product Rule
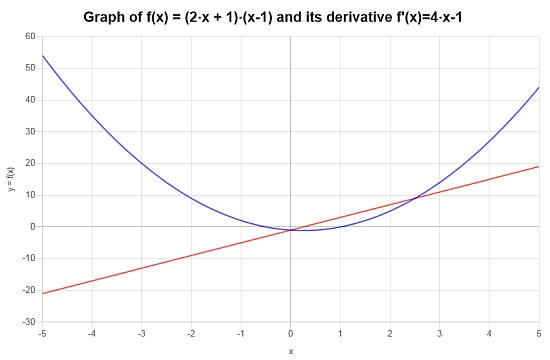
Calculate the derivative of: \(f(x) = (x-1)(2x+1) \)
Solution: We consider the following function \(\displaystyle f(x)=\left(x-1\right)\left(2x+1\right)\), which needs to be differentiated
.
\( \displaystyle \frac{d}{dx}\left(\left(2x+1\right)\left(x-1\right)\right)\)
By using the Product Rule: \(\frac{d}{dx}\left( \left(2x+1\right)\left(x-1\right) \right) = \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(2x+1\right) \cdot \left(x-1\right)+\left(2x+1 \right) \cdot \frac{d}{dx}\left(x-1\right)\)
By linearity, we know \(\frac{d}{dx}\left( x-1 \right) = \frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\) and \(\frac{d}{dx}\left( 2x+1 \right) = \frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)+\frac{d}{dx}\left(1\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)-\frac{d}{dx}\left(1\right)\right)\)
Since the derivative of a constant is 0, we find that:
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right) \left(\frac{d}{dx}\left(x\right)\right)\)
It is known that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(\frac{d}{dx}\left(2x\right)\right) \left(x-1\right)+\left(2x+1 \right)\)
So, we directly get: \(\frac{d}{dx}\left( 2x \right) = 2\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2\right) \left(x-1\right)+\left(2x+1 \right)\)
\( \displaystyle = \,\,\)
\(\displaystyle 2x+1+2\left(x-1\right)\)
Note that \((2) \cdot (x-1) = 2x-2\cdot 1 = 2x-2\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle 2x+1+2x-2\)
Grouping the terms with \(x\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2+2\right)x+1-2\)
Grouping together numerical values and operating the terms that were grouped with \(x\)
\( \displaystyle = \,\,\)
\(\displaystyle 4x+1-2\)
Reducing the integers that can be subtracted together: \(\displaystyle 1-2 = -1\)
\( \displaystyle = \,\,\)
\(\displaystyle 4x-1\)
Conclusion: Therefore, it is concluded that the derivative of the function is:
\[f'(x) = 4x-1\]
Graphically, the following plot depicts the situation:
Product Rule Examples
Find the derivative of: \(f(x) = x \sin(x)\)
Solution: In this example the given function is \(\displaystyle f(x)=x\sin\left(x\right)\). Let's find its derivative
\( \displaystyle \frac{d}{dx}\left(x\sin\left(x\right)\right)\)
We use the Product Rule: \(\frac{d}{dx}\left( x\sin\left(x\right) \right) = \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \frac{d}{dx}\left(\sin\left(x\right)\right)\)
By directly differentiating we find: \(\frac{d}{dx}\left( \sin\left(x\right) \right) = \cos\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(x\right) \cdot \sin\left(x\right)+x \cdot \cos\left(x\right)\)
So then after simplifying we get that:
\( \displaystyle = \,\,\)
\(\displaystyle x\cos\left(x\right)+\sin\left(x\right)\)
Conclusion: Hence, we find that the derivative is given by the following formula:
\[f'(x) = x\cos\left(x\right)+\sin\left(x\right)\]
The following graph is constructed for the function and its derivative:
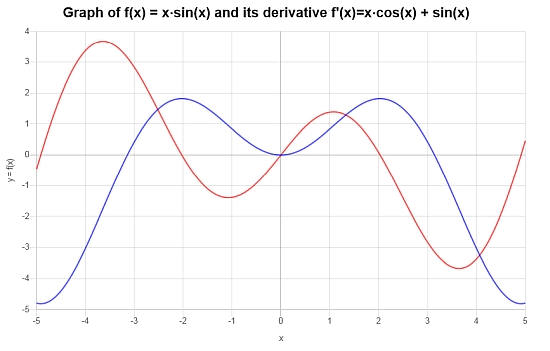
Example: Another Product Rule calculation
Differentiate the following function \( f(x) = x (x+1)^2 \).
Solution: Finally, for this example the given function is \(\displaystyle f(x)=x\left(x+1\right)^2\). Since there is a
product of function, we can use the product rule for differentiation.
\( \displaystyle \frac{d}{dx}\left(\left(x+1\right)^2x\right)\)
We use the Product Rule: \(\frac{d}{dx}\left( \left(x+1\right)^2x \right) = \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \cdot \frac{d}{dx}\left(x\right)\)
We know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \frac{d}{dx}\left(\left(x+1\right)^2\right) \cdot x+\left(x+1\right)^2 \)
Using the Power Rule for a constant exponent: \(\frac{d}{dx}\left( \left(x+1\right)^2 \right) = 2x+1\cdot \frac{d}{dx}\left(x+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\cdot \frac{d}{dx}\left(x+1\right)\right) x+\left(x+1\right)^2 \)
By linearity, we know \(\frac{d}{dx}\left( x+1 \right) = \frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\), so plugging that in:
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)+\frac{d}{dx}\left(1\right)\right)\right) x+\left(x+1\right)^2 \)
The derivative of a constant is 0, so then:
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\left(\frac{d}{dx}\left(x\right)\right)\right) x+\left(x+1\right)^2 \)
We know that \(\frac{d}{dx}\left(x\right) = 1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2x+1\right) x+\left(x+1\right)^2 \)
\( \displaystyle = \,\,\)
\(\displaystyle \left(x+1\right)^2+2\left(x+1\right)x\)
Expanding the terms: \(\left(x+1\right)^2 = \left(x+1\right)\left(x+1\right)\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(x+1\right)\left(x+1\right)+2\left(x+1\right)x\)
Observe that \((x+1) \cdot (x+1) = x^2+1x+1x+1^2 = x^2+2x+1\), as we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2\left(x+1\right)x\)
Note that \((x+1) \cdot (x) = x^2+1x = x^2+x\), due to the fact that we can use the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2\left(x^2+x\right)\)
We get \((2) \cdot (x^2+x) = 2x^2+2x = 2x^2+2x\), by using the distributive property on each term of the expression on the left, with respect to the terms on the right
\( \displaystyle = \,\,\)
\(\displaystyle x^2+2x+1+2x^2+2x\)
Grouping the terms with \(x\), \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(2+2\right)x+\left(1+2\right)x^2+1\)
Putting the integers together and simplifying the terms that were grouped with \(x\), \(x^2\)
\( \displaystyle = \,\,\)
\(\displaystyle 4x+3x^2+1\)
\( \displaystyle = \,\,\)
\(\displaystyle \left(3x+1\right)\left(x+1\right)\)
Conclusion: Based on what was calculated above, it is found that the corresponding derivative is:
\[f'(x) = \left(3x+1\right)\left(x+1\right)\]
The following plot is obtained for the given function on the interval \([-5, 5]\):
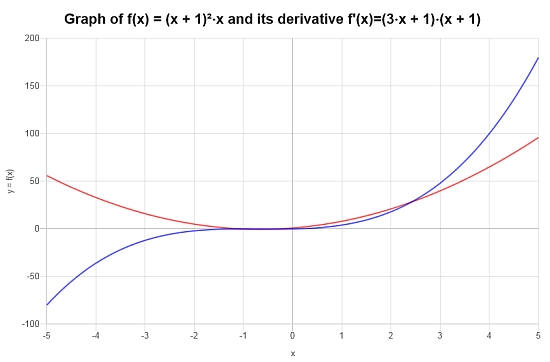
More derivative calculators
Few people will disagree that differentiation along with integration and central point of Calculus. Calculating a derivative is
a crucial skill that you will need to learn as a calculus student.
You can learn different 'flavors' of differentiation, including partial differentiation as well as
implicit differentiation, which are used in different application contexts.
Applications include tangent line calculation, which is the same as a linear approximation,
as well as the use of higher order derivatives, starting with second order derivatives.