More about this cos graph calculator

This calculator will allow you to generate the graph for any cosine function, along with the amplitude, period and frequency , showing all the steps. You need to provide a valid function involving the cosine function. It could be something trivial like cos(x), or you can make it more complicated like 2*cos(1/3 x + pi) - 4/5.

Once you provide a valid function involving cosine, just click on "Calculate" to get the results and all the steps of the process shown.

Cosine is one trigonometric function that has a myriad applications in Math and Physics. It is really commonly used also in Geometry, when solving triangles.

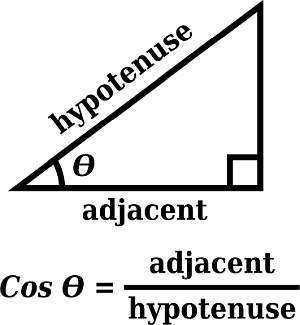
How to do a cos graph?

The main principle with graphing any type of function is to resort to a known simple function for which we know its graph, and then construct the graph we want to find based on translations and rescaling of this simple graph.

For the case of cos graph, we know that the simplest expression of a cosine function is f(x) = cos(x), which has a graph that is shown below:

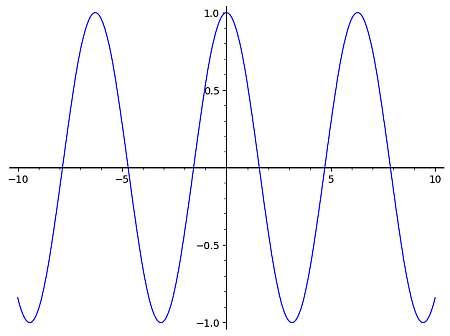
Then, we can use this base graph to derive the graph of more complex cos functions as the general shape will be the same, only that it can be potentially translated left or right, down or up, and the period can potentially change as well, depending on the function provided.

What are the steps for graphing a cosine function?

• Step 1: Identify the cos function you want to graph into the form a*cos(bx+c)+d if possible
• Step 2: The value of a will correspond to the amplitude, d is the units the basic cos graph is translated up, and the graph is shifted -c/b to the right
• Step 3: If the cos function is not in the form a*cos(bx+c)+d, then create a table of values for x and f(x) (where f(x) is the cos function given), and calculate several points that you can use to trace manually the shape of the cos graph

Indeed, only functions of the form a*cos(bx+c)+d will have a clear expression for amplitude, period, frequency and translations, but they are not the only cosine functions you can conceive of. For example, \(f(x) = cos(x^2)\) is a cos function, but it does not have period or frequency, for example.

Cos graph versus Sine graph?

How similar are the cosine and sine graphs? Well, pretty similar. First, notice that we are talking about the basic cos graph and sine graph, this is sin(x) and cos(x).

Then, the cos graph is obtained by simply shifting the sine graph to the left \(\pi/2\) units. So, the cos graph and sine graph are essentially the same, except for a translation.

Cos graph in degrees

Is there any difference between the cosine graph in radians and the cos graph in degrees? Well, there is a difference in scale, as cos completes a full period in \(2\pi\) when measured in radians, and it completes a full period in 360^o when measured in degrees. But in terms of the shape, there is no essential difference.

How to use this cos graph calculator?

This cos graph calculator eliminate all the guesswork for you, as all you have to do is to provide a valid cos function. Depending on the type of cos function you provide, you will have a period, or maybe the period won't be defined, in a case such as \(f(x) = cos(x^2)\), where we still say we have a cos function.

Cos graphs, along with sine and tangent graphs are among the most common trigonometric graphs that you will typically encounter.

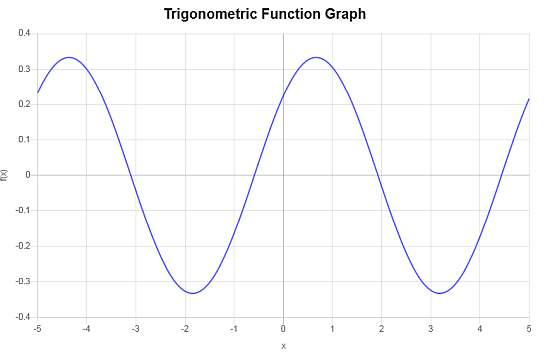
Example: Cos graph

Calculate the graph of : \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\)

Solution: The following function has been provided:

\[f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\]

Based on the argument of the trigonometric function that was passed, the frequency and the period are computed as follows:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

and also

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Therefore, considering the provided trigonometric function, \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x - \frac{5}{6}\right)\), we obtain that:

» The amplitude in this case is \(A = 1/3\).

» The phase shift is equal to \(\displaystyle\frac{\frac{5}{6}}{\frac{5}{4}} = 0.6667\).

» The vertical shift is equal to \( 0\).

Summarizing, the following has been found for the given trigonometric function

• Period = \(5.0265\)
• Frequency = \(0.1989\)
• Amplitude = \(1/3\)
• Phase Shift = \(0.6667\)
• Vertical Shift = \(\displaystyle 0\)

The following is the corresponding graph

Example: More cos graphs

Is the following function periodic? \(f(x) = \frac{1}{3} \cos\left( \frac{5}{4}x^2 - \frac{5}{6}\right)\)

Solution: No, it is not, because of the \(x^2\) term.

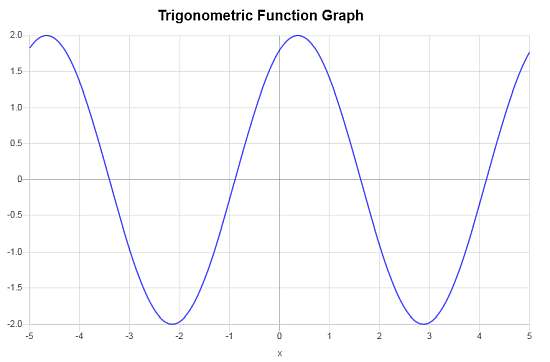
Example: Cosine graph

Calculate the graph of : \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\)

Solution: Notice that the passed trigonometric expression can be simplified as follows:

so then the function we will work with is \(f(x) = 2\cos\left(\frac{5}{4}x-\frac{11}{24}\right)\).

Hence, based on the argument of the trigonometric function that was passed, the frequency and the period are computed as follows:

\[ \begin{array}{ccl} \text{Period} & = & \displaystyle\frac{2\pi}{\frac{5}{4}} \\\\ \\\\ & \approx & 5.0265 \end{array}\]

and also

\[ \begin{array}{ccl} \text{Frequency} & = & \displaystyle\frac{\frac{5}{4}}{2\pi} \\\\ \\\\ & \approx & 0.1989 \end{array}\]

Based on the provided trigonometric function, \(f(x) = 2 \cos\left( \frac{5}{4}\left(x - \frac{7}{6}\right) + 1\right)\), we obtain that:

» The amplitude in this case is \(A = 2\).

» The phase shift is equal to \(\displaystyle\frac{\frac{11}{24}}{\frac{5}{4}} = 0.3667\).

» The vertical shift is equal to \( 0\).

Summarizing, the following has been found for the given trigonometric function

• Period = \(5.0265\)
• Frequency = \(0.1989\)
• Amplitude = \(2\)
• Phase Shift = \(0.3667\)
• Vertical Shift = \(\displaystyle 0\)

The following is the corresponding graph

More Geometry calculators

One of the most useful ones you can find is this period and frequency calculator, for which you provide any trigonometric function and you will get provided with the amplitude, period and frequency.

Also, you can use this sin calculator with steps to work with more complex trig expressions dealing with the sine function. Sine and cosine are indeed the cornerstone of all that is related with Geometry and Trigonometry

Also, perhaps you are interested in evaluating trig expressions or graphing trig functions in general.