Using Descartes Rule of Signs

This calculator will help you with the application of Descartes Rule of Signs, for any given polynomial that you provide. The only requirement for it is that the polynomial needs to be valid.

For example, you can provide simple cubic polynomial like x^3 - 2x + 1, but you can also provide a more complicated one, like x^5 - 3/4 x^4 - 1/7 x^3 + 2 x^2 + 2x + 1, etc.

Once you provide a valid polynomial function, you click on "Calculate" button, in order to get all the steps of the process shown.

Finding polynomial zeros is one of the most important tasks in Algebra, but it is not an easy task in general. There are no general formulas for all polynomials of all degrees, so we usually have to follow a systematic procedure to find as many roots as we can.

In this context, having as much information about the type of roots available is always useful, and that is one the objectives of Descartes Rule of Signs.

Is Descartes rule of signs important?

Yes, it is! But more from a historical context than anything else, and as a theoretical proof of concept of how powerful properties can be derived from simple conditions.

From an operational point of view, Descartes rule of signs is not used by algebraic calculators nor computers when you compute roots of a polynomial.

So then, Descartes Rule of signs is a very interesting properties that can tell you a lot about the roots of a polynomial, without doing any calculation really, for which reason is a really practical tool to use.

What is Descartes rule of change?

Like the name states, this rule compute sign changes between consecutive coefficients of a polynomials. The number of changes found will tell you some information about the number of positive and negative roots.

Why would you want to know about the number of positive and negative roots, when you can use your calculator to get ALL the roots? True, but what if you don't have your calculator with you, how do you do it? Descartes Rule of Signs can help you.

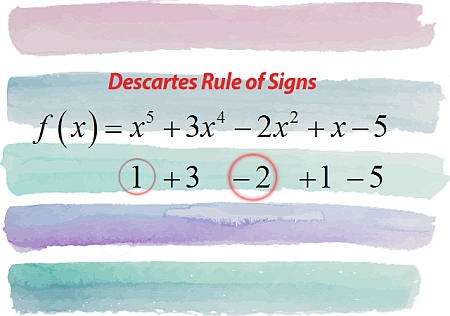
What does the Descartes Rule of Signs State?

In simple terms, the Descartes Rule of Signs tells you something about the number of positive and negative roots of a polynomial, by just looking at the signs of the coefficients of the given polynomial.

More precisely, you start with the leading coefficient, and you ignore zero coefficients, and go counting changes in sign. The total number of changes in the sign of consecutive coefficients is an upper bound for the number of positive roots of \(p(x)\), and the number of positive roots has the same parity as the total number of changes in signs.

Then, you do the same exercise, but for the coefficients of \(p(-x)\), and what you get in that case is that total number of changes in the sign of consecutive coefficients is an upper bound for the number of negative roots of \(p(x)\), and the number of negative roots has the same parity as the total number of changes in sign.

Steps for applying Descartes Rule of Signs

• Step 1: Identify the polynomial p(x) you need to analyze. Make sure it is a polynomial (otherwise the method does not work) and simplify it as much as possible
• Step 2: Put the coefficients of p(x) in a row, starting from the leading coefficient, in descending order and omitting zero coefficients
• Step 3: Starting from the leading coefficient, count the sign changes between consecutive coefficients, and take note of the total number of sign changes, and call it T
• Step 4: The number of positive zeros of p(x) is at most T and it has the same parity as T (if T is even, then the number of positive zeros of p(x) is an even number, and if T is odd, then the number of positive zeros of p(x) is an odd number)
• Step 4: Repeat the same process now for the coefficients of p(-x), to get information about the number of negative zeros of p(x)

This method can give you potentially a range of possible values for the number of positive (and negative) zeros, but it can also potentially tell you EXACTLY how many positive (or negative) zeros a given polynomial has, depending only on how many sign changes you count.

Can I calculate the actual zeros with this method?

No, Descartes Rule of Signs is not intended to give you information about what the actual roots are, it only tells you something about the NUMBER of positive (and negative) roots.

Now, combining this information, with the rational root theorem and other elementary tools, including synthetic division and the factor theorem, you will be better equipped for looking at the actual value of the roots.

Tips and Tricks

Always simplify the polynomial first. For example, if you have \(p(x) = x^5 - x^3\), you will want to first to \(p(x) = x^5 - x^3 = x^3(x^2 - 1)\), so then you know that 0 is a root (with multiplicity 3), and you apply Descartes rule to \(x^2 - 1\) instead.

Example: Descartes Rule of Signs

Indicate the possible number of positive and negative roots of \(x^4 - x^3 + x^2 + 1\)

Solution: We are provided with the following polynomial function: \(\displaystyle x^4 - x^3 + x^2 + 1\), for which we need to apply Descartes Rule of Signs.

Positive Roots: The polynomial coefficients (for higher to lower power) are:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,+1\,\,\]

We find that the number of sign changes in consecutive coefficients is: \(2\), and the changes are: \(\,\,+1\,\,\) and\(\,\,-1\,\,\), \(\,\,-1\,\,\) and\(\,\,+1\,\,\).

Negative Roots: The polynomial coefficients for \(p(-x) = x^4+x^3+x^2+1\) are:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,+1\,\,\]

No sign changes are found for the coefficients of \(p(-x)\).

Conclusion: Based on the number of sign changes found, which is \(2\), we conclude that \(p(x)\) can have 0 or 2 positive roots for \(p(x) = x^4-x^3+x^2+1\).

Now, since no sign changes were found for the coefficients of \(p(-x)\), we conclude that there are NO negative zeros for \(p(x) = x^4-x^3+x^2+1\).

Example: More of Descartes Sign Rule

Indicate the possible number of positive and negative roots of \(x^4 + x^3 + x^2 - 1\)

Solution: Now we need to analyze \(\displaystyle x^4 + x^3 + x^2 - 1\), with Descartes Rule of Signs.

The provided expression is already simplified, so there is nothing further to simplify.

Positive Roots: The coefficients are:

\[\,\,+1\,\, \,\,+1\,\, \,\,+1\,\, \,\,-1\,\,\]

Observe that the number of sign changes in consecutive coefficients in this case is equal to \(1\), and the changes are: \(\,\,+1\,\,\) and\(\,\,-1\,\,\).

Negative Roots: The polynomial coefficients associated to \(p(-x) = x^4-x^3+x^2-1\) are:

\[\,\,+1\,\, \,\,-1\,\, \,\,+1\,\, \,\,-1\,\,\]

Then, the number of sign changes in consecutive coefficients is equa to \(3\), and the changes are: \(\,\,+1\,\,\) and \(\,\,-1\,\,\), \(\,\,-1\,\,\) and \(\,\,+1\,\,\), \(\,\,+1\,\,\) and\(\,\,-1\,\,\)

Conclusion: Since there is one sign change among the coefficients of \(p(x)\), we conclude that there is exactly ONE positive zero for \(p(x) = x^4+x^3+x^2-1\).

Based on the number of sign changes found, which is \(3\), we conclude that \(p(x) = x^4+x^3+x^2-1\) can have 1 or 3 negative roots.

Example: Positive and Negative signs

Indicate the possible number of positive and negative roots of \(x^4 + 1\). Can you say something the precise number of positive and negative roots?

Solution: In this case there are no sign changes so then there are no positive roots. Now, \(p(-x) = (-x)^4 + 1 = x^4 + 1\), which does not have sign changes, so then there are no negative roots either. The conclusion is that polynomial does not have real roots (since 0 is not a root either).

More Polynomial calculators

Finding polynomial roots is one the central points for most application problems in Calculus and Algebra, and it is a skill worth mastering.

There are many skills involved in the calculation of zeros of a polynomial, and Descartes Signs Rule gives you a lot of information that can be inferred really simply by looking at the polynomial's coefficients.